„Termodinamika példák - Lineáris hőmérsékletprofil” változatai közötti eltérés
A Fizipedia wikiből
a (→Feladat) |
a |
||
| (egy szerkesztő 5 közbeeső változata nincs mutatva) | |||
| 6. sor: | 6. sor: | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| gyaksorszám = 1 | | gyaksorszám = 1 | ||
| − | |||
| témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | | témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | ||
| − | | | + | | rövid = Kinetikus gázelmélet, transzport |
| − | + | ||
| − | + | ||
| − | + | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| 17. sor: | 13. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A $j_z=-\lambda \frac{\mathrm{d}T}{\mathrm{d}z}$ | + | <wlatex>A $j_z=-\lambda \frac{\mathrm{d}T}{\mathrm{d}z}$ hőáramsűrűségre felírt egyenletet vonatkoztassuk most egy rögzített $A$ keresztmetszetre, így a $J_Q=\frac{\mathrm{d}Q}{\mathrm{d}t}$ hőáramot ($A$ felületen átadott hőteljesítményt) kapjuk: |
| − | $$\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}$$ | + | $$ \frac{\mathrm{d}Q}{\mathrm{d}t} = -\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}. $$ |
| − | + | Stacionárius esetben hő nem halmozódhat fel, $J_Q$ állandó minden az eredeti két felülettel párhuzamos keresztmetszetre, bármely $z$ magasságban legyen is az. | |
| + | Mivel a keresztmetszet $A$ nagysága állandó, $\frac{\mathrm{d}T}{\mathrm{d}z}$ is állandó, aminek általános megoldása $T(z) = T_0 + c_T z$ lineáris függvény. | ||
| − | + | A $T(0)=T_1,\,T(d)=T_2$ peremfeltételekre illesztve a hőmérsékletprofil | |
| − | + | $$ T(z) = T_1+\frac{T_2-T_1}{d}z. $$ | |
| − | + | ||
| − | + | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. április 27., 10:43-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó 
és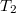 
, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért 
távolsággal, és írjuk fel a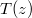 
függvényt a megadott mennyiségekkel!
Megoldás
A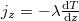 
hőáramsűrűségre felírt egyenletet vonatkoztassuk most egy rögzített 
keresztmetszetre, így a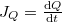 
hőáramot ( felületen átadott hőteljesítményt) kapjuk:
![\[ \frac{\mathrm{d}Q}{\mathrm{d}t} = -\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}. \]](/images/math/a/d/f/adf072f01a93b88fafcca5746e66c8b7.png)
Stacionárius esetben hő nem halmozódhat fel,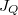 
állandó minden az eredeti két felülettel párhuzamos keresztmetszetre, bármely magasságban legyen is az.
Mivel a keresztmetszet nagysága állandó,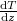 
is állandó, aminek általános megoldása 
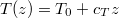lineáris függvény.
A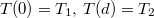 
peremfeltételekre illesztve a hőmérsékletprofil
![\[ T(z) = T_1+\frac{T_2-T_1}{d}z. \]](/images/math/7/4/c/74c38e107d335c44f42b2d14350ff875.png)
