„Termodinamika példák - Fűtött szoba belső energiája” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika {{Kísérleti fizika gyakorlat | tárgynév …”) |
a (Szöveg koherenssé tétele) |
||
| (egy szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy $V$ térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson $T_1$-ről $T_2$-re nő. Mennyivel változik a szobában lévő levegő belső energiája?</wlatex><noinclude> | + | </noinclude><wlatex># Egy $V$ térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson $T_1$-ről $T_2$-re nő. Mennyivel változik a szobában lévő levegő belső energiája?</wlatex><includeonly><wlatex>{{Végeredmény|content=Nem változik.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Ideális gáz esetén állandó anyagmennyiségnél $\frac{pV}{T}=Nk=\mathrm{const.}$, ami itt nem teljesül, mert a nyílászárókon át a melegítés hatására levegő távozik, a nyomás mindvégig egyenlő a környezeti nyomással. A fűtés hatására a szoba térfogatváltozása elhanyagolható. |
| + | |||
| + | $$ N k T = p V = p_\text{körny} V_\text{szoba} = \mathrm{const.}, $$ | ||
| + | azaz $ N = \frac{\mathrm{const.}}{T}$, és a belső energia kifejezhető | ||
| + | $$ U = \frac{f}{2} NkT $$ | ||
| + | alakban, amiről éppen most láttuk be, hogy nem változik. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. április 28., 17:04-kori változata
Feladat
- Egy
térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson 
-ről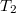 
-re nő. Mennyivel változik a szobában lévő levegő belső energiája?
Megoldás
Ideális gáz esetén állandó anyagmennyiségnél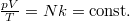 
, ami itt nem teljesül, mert a nyílászárókon át a melegítés hatására levegő távozik, a nyomás mindvégig egyenlő a környezeti nyomással. A fűtés hatására a szoba térfogatváltozása elhanyagolható.
![\[ N k T = p V = p_\text{körny} V_\text{szoba} = \mathrm{const.}, \]](/images/math/b/6/9/b692bd33f9317399d1e22621321071b5.png)
azaz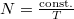 
, és a belső energia kifejezhető
![\[ U = \frac{f}{2} NkT \]](/images/math/7/3/2/732dd2f182a1531ef592333f02be51de.png)
alakban, amiről éppen most láttuk be, hogy nem változik.
