„Termodinamika példák - Kondenzált anyag közelítő állapotegyenlete” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika {{Kísérleti fizika gyakorlat | tárgynév …”)
 
a (Szöveg koherenssé tétele.)
 
(egy szerkesztő egy közbeeső változata nincs mutatva)
10. sor: 10. sor:
 
== Feladat ==
 
== Feladat ==
 
</noinclude><wlatex># Kondenzált (folyadék vagy szilárd) anyagok egyik közelítő állapotegyenlete $$V= V_0(1-ap+bT).$$ Mi az $a$ és $b$ paraméterek jelentése?</wlatex><includeonly><wlatex>{{Végeredmény|content=$V_0$ térfogatnál érvényes izotermikus kompresszibilitás és hőtágulási együttható.}}</wlatex></includeonly><noinclude>
 
</noinclude><wlatex># Kondenzált (folyadék vagy szilárd) anyagok egyik közelítő állapotegyenlete $$V= V_0(1-ap+bT).$$ Mi az $a$ és $b$ paraméterek jelentése?</wlatex><includeonly><wlatex>{{Végeredmény|content=$V_0$ térfogatnál érvényes izotermikus kompresszibilitás és hőtágulási együttható.}}</wlatex></includeonly><noinclude>
 +
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege.
+
<wlatex>Ha a térfogat nyomás- és hőmérsékletfüggését megvizsgáljuk, rendre azt találjuk, hogy
 +
$$ \left(\frac{\partial V}{\partial p}\right)_T=-a V_0, \qquad \left(\frac{\partial V}{\partial T}\right)_p=b V_0. $$
 +
 
 +
Ezeket a kifejezéseket a megszokott
 +
$$ \kappa_T = -\frac{1}{V_0} \left(\frac{\partial V}{\partial p}\right)_T, \qquad \beta_p = \frac{1}{V_0} \left(\frac{\partial V}{\partial T}\right)_p $$
 +
definíciókkal összevetve észrevehetjük, hogy $a$ és $b$ rendre a $V_0$ térfogat környezetében érvényes
 +
izoterm kompresszibilitás és izobár hőtágulási együttható.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2013. április 29., 10:01-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Állapotváltozás, I. főtétel
Feladatok listája:
  1. Állapotváltozások diagramjai
  2. Belső energia állapotváltozásokban
  3. Energiák fajhőviszonnyal
  4. Energiaváltozások diagramból
  5. Ideális gáz kompresszibilitásai
  6. Nyomás hőmérsékletfüggése
  7. Fűtött szoba belső energiája
  8. Térfogatváltozás fajhőviszonnyal
  9. Van der Waals-gáz egyensúlya
  10. Közelítő állapotegyenlet
  11. Állapotegy. mérh. menny.-ből
  12. Van der Waals-gáz fajhőkülönbsége
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Kondenzált (folyadék vagy szilárd) anyagok egyik közelítő állapotegyenlete
    \[V= V_0(1-ap+bT).\]
    Mi az \setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0% paraméterek jelentése?

Megoldás

Ha a térfogat nyomás- és hőmérsékletfüggését megvizsgáljuk, rendre azt találjuk, hogy

\[ \left(\frac{\partial V}{\partial p}\right)_T=-a V_0, \qquad \left(\frac{\partial V}{\partial T}\right)_p=b V_0. \]

Ezeket a kifejezéseket a megszokott

\[ \kappa_T = -\frac{1}{V_0} \left(\frac{\partial V}{\partial p}\right)_T, \qquad \beta_p = \frac{1}{V_0} \left(\frac{\partial V}{\partial T}\right)_p \]

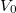definíciókkal összevetve észrevehetjük, hogy \setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0% rendre a \setbox0\hbox{$V_0$}% \message{//depth:\the\dp0//}% \box0% térfogat környezetében érvényes izoterm kompresszibilitás és izobár hőtágulási együttható.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Kondenzált_anyag_közelítő_állapotegyenlete&oldid=9644”