„Termodinamika - Entrópia, II. főtétel” változatai közötti eltérés
A Fizipedia wikiből
a (Olvashatóság javítása kiemeléssel) |
|||
| (egy szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| + | <noinclude> | ||
[[Kategória:Kísérleti fizika 3. gyakorlat]] | [[Kategória:Kísérleti fizika 3. gyakorlat]] | ||
[[Kategória:Szerkesztő:Stippinger]] | [[Kategória:Szerkesztő:Stippinger]] | ||
| 5. sor: | 6. sor: | ||
| gyaksorszám = 4 | | gyaksorszám = 4 | ||
| témakör = Termodinamika - Entrópia, II. főtétel | | témakör = Termodinamika - Entrópia, II. főtétel | ||
| + | | fejezetlap = true | ||
}} | }} | ||
== Az entrópia == | == Az entrópia == | ||
| − | <wlatex>Az entrópiaváltozás általános definíciója | + | <wlatex>'''Az entrópiaváltozás általános definíciója''' |
$$ \mathrm{d}S = \frac{\delta Q}{T}, $$ | $$ \mathrm{d}S = \frac{\delta Q}{T}, $$ | ||
ahol az I. főtételből kifejezhetjük a közölt hőt: | ahol az I. főtételből kifejezhetjük a közölt hőt: | ||
$$ \mathrm{d}S= C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. $$ | $$ \mathrm{d}S= C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. $$ | ||
| − | Spontán folyamatokban $\mathrm{d}S\geq0$, reverzíbilis folyamatokban $\mathrm{d}S=0$, irreverzíbilis folyamatokban $\mathrm{d}S>0$.</wlatex> | + | Spontán folyamatokban $\mathrm{d}S\geq0$, reverzíbilis folyamatokban $\mathrm{d}S=0$, irreverzíbilis folyamatokban $\mathrm{d}S>0$. |
| + | |||
| + | '''A termodinamika II. főtétele''' kimondja, hogy egy periodikusan működő hőerőgép $\eta = \frac{Q_\text{fel}-Q_\text{le}}{Q_\text{fel}}$ hatásfoka mindig kisebb $1$-nél: $\eta<1$. | ||
| + | |||
| + | '''A termodinamika III. főtétele''' kimondja, hogy homogén szilárd és folyékony anyagok entrópiája az abszolút nulla hőmérséklethez közeledve nullához tart: $S(0)=0$.</wlatex> | ||
== Feladatok == | == Feladatok == | ||
| + | </noinclude> | ||
{{:Termodinamika példák - Entrópiaváltozás izoterm táguláskor}}{{Megoldás|link=Termodinamika példák - Entrópiaváltozás izoterm táguláskor}} | {{:Termodinamika példák - Entrópiaváltozás izoterm táguláskor}}{{Megoldás|link=Termodinamika példák - Entrópiaváltozás izoterm táguláskor}} | ||
{{:Termodinamika példák - Entrópiaváltozás izobár táguláskor}}{{Megoldás|link=Termodinamika példák - Entrópiaváltozás izobár táguláskor}} | {{:Termodinamika példák - Entrópiaváltozás izobár táguláskor}}{{Megoldás|link=Termodinamika példák - Entrópiaváltozás izobár táguláskor}} | ||
A lap jelenlegi, 2013. május 4., 23:23-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Az entrópia
Az entrópiaváltozás általános definíciója
![\[ \mathrm{d}S = \frac{\delta Q}{T}, \]](/images/math/c/b/d/cbd5cf7c09169ef24d1244b4e66f68f5.png)
ahol az I. főtételből kifejezhetjük a közölt hőt:
![\[ \mathrm{d}S= C_V \frac{\mathrm{d}T}{T} + \frac{p\,\mathrm{d}V}{T}. \]](/images/math/9/2/d/92d483cebee56f48a4e75a0814ddd76e.png)
Spontán folyamatokban 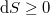 , reverzíbilis folyamatokban
, reverzíbilis folyamatokban 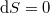 , irreverzíbilis folyamatokban
, irreverzíbilis folyamatokban 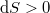 .
.
A termodinamika II. főtétele kimondja, hogy egy periodikusan működő hőerőgép 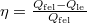 hatásfoka mindig kisebb
hatásfoka mindig kisebb  -nél:
-nél: 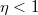 .
.
A termodinamika III. főtétele kimondja, hogy homogén szilárd és folyékony anyagok entrópiája az abszolút nulla hőmérséklethez közeledve nullához tart: 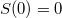 .
.
Feladatok
-
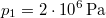 nyomású,
nyomású, 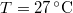 hőmérsékletű és
hőmérsékletű és 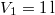 térfogatú ideális gáz izotermikusan
térfogatú ideális gáz izotermikusan 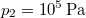 nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája?
nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája?
- Mennyivel változik meg
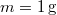 nitrogéngáz entrópiája, ha állandó nyomáson
nitrogéngáz entrópiája, ha állandó nyomáson 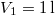 térfogatról
térfogatról 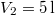 térfogatra expandáltatjuk.
térfogatra expandáltatjuk.
- Tekintsünk
 tömegű,
tömegű,  móltömegű,
móltömegű,  fajhőviszonyú ideális gázt.
fajhőviszonyú ideális gázt.
- a) Vezesse le az entrópia hőmérséklet- és térfogatfüggését megadó összefüggést!
- b) A kapott entrópia-kifejezés segítségével vezesse le az adiabata egyenletét!
- Az ideális gáz entrópiáját gyakran az
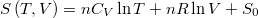 alakban használják.
alakban használják.
- a) Indokolja meg, hogy az
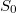 mennyiségnek függnie kell a rendszer anyagmennyiségét megadó
mennyiségnek függnie kell a rendszer anyagmennyiségét megadó  mólszámtól!
mólszámtól!
- b) Adjon meg egy olyan
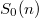 -függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!
-függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!
- a) Indokolja meg, hogy az
-
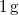
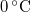 -os víz állandó nyomáson
-os víz állandó nyomáson 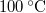 -os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!.
-os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!.
-
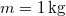 tömegű,
tömegű, 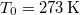 hőmérsékletű vizet termikus kapcsolatba hozunk egy
hőmérsékletű vizet termikus kapcsolatba hozunk egy 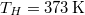 hőmérsékletű hőtartállyal.
hőmérsékletű hőtartállyal.
- a) Mekkora a víz entrópia-változása, miután a hőmérséklete elérte a hőtartály hőmérsékletét?
- b) Mekkora eközben a hőtartály entrópia-változása?
- c) Mekkora a teljes rendszerben (hőtartály és víz) létrejött entrópia-változás?
- d) Mennyi a teljes rendszerben létrejött entrópia-változás, ha a testet először egy
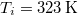 hőmérsékletű hőtartállyal, majd az egyensúly beállta után a
hőmérsékletű hőtartállyal, majd az egyensúly beállta után a 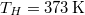 hőmérsékletű hőtartállyal hozzuk kapcsolatba?
hőmérsékletű hőtartállyal hozzuk kapcsolatba?
- e) Lehet-e úgy melegíteni a vizet, hogy a teljes rendszer entrópia-változása kisebb legyen egy előírt értéknél (vagyis a folyamat előírt mértékben megközelítse a reverzíbilis folyamatot)?
- Tekintsünk ideális gázzal végzett Carnot-körfolyamatot.
- a) Ábrázoljuk a Carnot-körfolyamatot
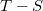 diagramban!
diagramban!
- b) Mutassuk ki, hogy a körfolyamatban a gáz által végzett munka most is a körfolyamat területével egyenlő!
- c) Számítsuk ki a fentiek alapján a Carnot-körfolyamat hatásfokát!
- a) Ábrázoljuk a Carnot-körfolyamatot
- Egymástól válaszfallal elzárt,
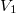 és
és 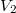 térfogatú két edényben azonos hőmérsékletű, azonos nyomású,
térfogatú két edényben azonos hőmérsékletű, azonos nyomású, 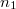 és
és 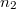 mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
- a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!
- b) Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok
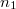 és
és 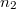 mólszámaival!
mólszámaival!
- c) Számítsuk ki az entrópia-változást, ha a két edényben azonos fajtájú gáz van!
-
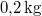 ,
, 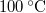 hőmérsékletű vasat hőszigetelt kaloriméterben lévő,
hőmérsékletű vasat hőszigetelt kaloriméterben lévő, 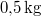 ,
, 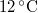 -os vízbe teszünk. A vas fajhője
-os vízbe teszünk. A vas fajhője 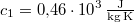 , a vízé
, a vízé 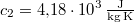 . Mennyi az entrópiaváltozás a hőmérséklet kiegyenlítődése miatt, ha a nyomás állandó?
. Mennyi az entrópiaváltozás a hőmérséklet kiegyenlítődése miatt, ha a nyomás állandó?
- Két test azonos
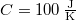 hőkapacitású, de hőmérsékletük különböző:
hőkapacitású, de hőmérsékletük különböző: 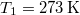 ,
, 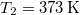 .
.
- a) Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?
- b) Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?
- c) Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?
![\[\Delta S=\frac{p_1 V_1}{T}\ln\frac{p_1}{p_2}=19{,}97\,\mathrm{\frac{J}{K}}\]](/images/math/6/d/0/6d0b864aa264a9c16325151512c98203.png)
![\[\Delta S=\frac{m}{\mu_\mathrm{N_2}}C_p\ln\frac{V_2}{V_1}=3{,}34\,\mathrm{\frac{J}{K}}, \qquad C_p=\frac72R.\]](/images/math/6/9/3/69379145baf5ca7bc790fdc4464b8173.png)
![\[S=\frac{m}{M}R\ln\left(T^{\frac{1}{\gamma-1}}V\right)+S_0\]](/images/math/7/0/3/703497cb4e3daf33126d8a9df9ebb08d.png)
![\[TV^{\gamma-1}=\mathrm{const.}\]](/images/math/7/5/4/754140f6a21d584b63f5d26d9a18a297.png)
![\[S_0(n)=-nR\ln n+ns_0,\]](/images/math/0/f/5/0f5e8e66063357f77affc5dd75e82760.png)
![\[S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,\]](/images/math/e/5/8/e580690ef414387f9272cc6ffe11e430.png)
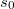 már
már ![\[\Delta S = mc\ln\frac{373}{273}+\frac{mL_f}{373\,\mathrm{K}}=7{,}36\,\mathrm{\frac{J}{K}},\]](/images/math/8/f/f/8ff47ef68c48ff988ac413b430356235.png)
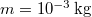 a víz tömege,
a víz tömege,  a víz fajhője,
a víz fajhője, 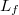 a forráshője.
a forráshője. ![\[1306\,\mathrm{\frac{J}{K}}\]](/images/math/2/d/8/2d8871a7637fa7346587bd1eb82a4c69.png)
![\[-1121\,\mathrm{\frac{J}{K}}\]](/images/math/0/3/9/039511937396c1ce27cf7b567a919c69.png)
![\[185\,\mathrm{\frac{J}{K}}\]](/images/math/0/6/1/06120b7dea96d50e3214e101a83a9563.png)
![\[98\,\mathrm{\frac{J}{K}}\]](/images/math/9/2/9/929c0bc6fa4c0264edcf460bb60e5c28.png)
![\[\Delta S = R n_1 \ln\frac{n_1+n_1}{n_1} + R n_2 \ln\frac{n_1+n_2}{n_2}\]](/images/math/5/9/6/596d530da1c94e91161150cb929bb191.png)
![\[\Delta S=0\]](/images/math/8/1/c/81ca578b10374e17bce8368f5500ff49.png)
![\[T_k=288{,}7\,\mathrm{K},\qquad \Delta S=3{,}41\,\mathrm{\frac{J}{K}}\]](/images/math/b/d/b/bdb4a99b8fe7577d94178ef75c691ba3.png)
![\[T_k=\frac{T_1+T_2}{2}\]](/images/math/e/4/0/e40444a3f717bb0150a6cddb411c076d.png)
![\[T_k=\sqrt{T_1 T_2}\]](/images/math/2/2/5/22549fc9b794cce58ca4c0f18c2725c4.png)
![\[\Delta U_a=0, \qquad \Delta U_b=2C\sqrt{T_1 T_2}-CT_1-CT_2=-778{,}7\,\mathrm{J},\]](/images/math/4/4/a/44a431f68a2caaec70e8da0364f277ff.png)
![\[\Delta S_a=2C\ln\frac{T_1+T_2}{2}-C\ln T_1-C\ln T_2=2{,}42\,\mathrm{\frac{J}{K}}, \qquad \Delta S_b=0.\]](/images/math/7/a/1/7a11e8b14bc0459f04ada0abf724dd1b.png)