„Termodinamika példák - Gáz szökése” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 6. sor: | 6. sor: | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| gyaksorszám = 1 | | gyaksorszám = 1 | ||
| − | |||
| témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | | témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | ||
| − | | | + | | rövid = Kinetikus gázelmélet, transzport |
| − | + | ||
| − | + | ||
| − | + | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># $V$ térfogatú, vékonyfalú tartályban ideális gáz van, az edényt légüres tér veszi körül. Feltesszük, hogy a gáz kiáramlása lassú, így a gáz egyensúlyi állapotát a folyamat nem zavarja, továbbá a lyuk mérete sokkal kisebb, mint a szabad úthossz, tehát a lyuk területére is érvényes az az összefüggés, hogy az edény falának időegység alatt nekiütköző molekulák | + | </noinclude><wlatex># $V$ térfogatú, vékonyfalú tartályban ideális gáz van, az edényt légüres tér veszi körül. Feltesszük, hogy a gáz kiáramlása lassú, így a gáz egyensúlyi állapotát a folyamat nem zavarja, továbbá a lyuk mérete sokkal kisebb, mint a szabad úthossz, tehát a lyuk területére is érvényes az az összefüggés, hogy az edény falának időegység alatt nekiütköző molekulák száma $\frac{1}{4}n_V A\langle v\rangle$, ahol $\langle v\rangle$ a molekulák átlagsebessége. A hőmérséklet mindvégig $T$.</wlatex> |
#* <wlatex>a) Hogyan változik az idő függvényében az edényben lévő gáz $N$ részecskeszáma, ha a tartály falán igen kicsi, $A$ területű lyuk van?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$N(t)=n_0\exp\{-t/\tau\},$$ ahol $N_0$ a kezdeti részecskeszám-sűrűség, $\tau=\frac{4V}{A\langle v\rangle}$.}}</wlatex></includeonly> | #* <wlatex>a) Hogyan változik az idő függvényében az edényben lévő gáz $N$ részecskeszáma, ha a tartály falán igen kicsi, $A$ területű lyuk van?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$N(t)=n_0\exp\{-t/\tau\},$$ ahol $N_0$ a kezdeti részecskeszám-sűrűség, $\tau=\frac{4V}{A\langle v\rangle}$.}}</wlatex></includeonly> | ||
#* <wlatex>b) Határozzuk meg azt az időtartamot, amely alatt a gáz nyomása felére csökken!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\tau_{1/2}=\tau \ln 2$$}}</wlatex></includeonly><noinclude> | #* <wlatex>b) Határozzuk meg azt az időtartamot, amely alatt a gáz nyomása felére csökken!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\tau_{1/2}=\tau \ln 2$$}}</wlatex></includeonly><noinclude> | ||
| 25. sor: | 21. sor: | ||
ahol $\displaystyle \tau=\frac{A \langle v \rangle}{4V}$ a folyamat karakterisztikus ideje. | ahol $\displaystyle \tau=\frac{A \langle v \rangle}{4V}$ a folyamat karakterisztikus ideje. | ||
| − | + | '''a)''' A tartályban lévő molekulák száma az idő függvényében | |
| − | + | $$N(t)=V n_V(t)=n_{V0}\exp\left\{-\frac{t}{\tau}\right\}.$$ | |
| − | + | ||
| + | '''b)''' A molekulák számának felezési idejét | ||
$$ n_V\left(t_{1/2}\right) = \frac{n_{V0}}{2} $$ | $$ n_V\left(t_{1/2}\right) = \frac{n_{V0}}{2} $$ | ||
egyenletből számítjuk ki: | egyenletből számítjuk ki: | ||
A lap jelenlegi, 2013. április 26., 21:56-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
térfogatú, vékonyfalú tartályban ideális gáz van, az edényt légüres tér veszi körül. Feltesszük, hogy a gáz kiáramlása lassú, így a gáz egyensúlyi állapotát a folyamat nem zavarja, továbbá a lyuk mérete sokkal kisebb, mint a szabad úthossz, tehát a lyuk területére is érvényes az az összefüggés, hogy az edény falának időegység alatt nekiütköző molekulák száma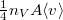 
, ahol 
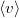a molekulák átlagsebessége. A hőmérséklet mindvégig 
.
- a) Hogyan változik az idő függvényében az edényben lévő gáz
részecskeszáma, ha a tartály falán igen kicsi, 
területű lyuk van?
- b) Határozzuk meg azt az időtartamot, amely alatt a gáz nyomása felére csökken!
- a) Hogyan változik az idő függvényében az edényben lévő gáz
Megoldás
Amikor a gáz kis lyukon keresztül szökik a tartályból, feltehetjük, hogy végig egyensúlyi állapotban marad. A lyukon keresztül időegység alatt távozó molekulák száma pedig megegyezik azzal, amit a gáz kinetikus elméletében a nyomás tárgyalásakor az edény falának egységnyi felületét időegység alatt érő molekulák számára kapunk. Mivel a molekulák száma időben változik, ezért differenciálegyenletet kapunk a tartályban lévő molekulák időfüggő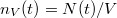 
sűrűségére:
![\[-\frac{\mathrm{d}N}{\mathrm{d}t}=V\frac{\mathrm{d}n_V}{\mathrm dt}=-\frac14 n_V A \langle v \rangle.\]](/images/math/1/3/5/135e5e97173ce34234bb8ff5ecd96dcd.png)
A kapott differenciálegyenlet a változók szétválasztással megoldható:
![\[-\frac{\mathrm{d}n_V}{n_V}=-\frac{A \langle v \rangle}{4V}\,\mathrm{d}t,\]](/images/math/1/d/4/1d44d41286719e2a1f0308448f71b9e5.png)
![\[\ln \frac{n_V}{n_{V0}}=-\frac{t}{\tau},\]](/images/math/a/3/7/a3724d8444d94d007e72f78edaa7b6e0.png)
ahol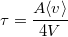 
a folyamat karakterisztikus ideje.
a) A tartályban lévő molekulák száma az idő függvényében
![\[N(t)=V n_V(t)=n_{V0}\exp\left\{-\frac{t}{\tau}\right\}.\]](/images/math/9/4/5/945f1893537623a8ac2d1ae69392d853.png)
b) A molekulák számának felezési idejét
![\[ n_V\left(t_{1/2}\right) = \frac{n_{V0}}{2} \]](/images/math/d/2/4/d247656571fccbfeeff09b0b954d958a.png)
egyenletből számítjuk ki:
![\[ t_{1/2} = \tau \ln 2.\]](/images/math/1/4/2/142752eb54dbd6995c254716cd50494e.png)
