„Termodinamika példák - Jég fagyása” változatai közötti eltérés
A Fizipedia wikiből
a (Tördelés fejlesztése.) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 6. sor: | 6. sor: | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| gyaksorszám = 1 | | gyaksorszám = 1 | ||
| − | |||
| témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | | témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok | ||
| − | | | + | | rövid = Kinetikus gázelmélet, transzport |
| − | + | ||
| − | + | ||
| − | + | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Mennyi idő alatt képződik $Z=5\,\mathrm{cm}$ vastag jégréteg egy tó felszínén, ha a léghőmérséklet $T_\ell=-10\,\mathrm{^\circ C}$, a víz hőmérséklete a jégréteg alatt $T_0=0\,\mathrm{^\circ C}$? Tegyük fel, hogy a jégréteg felső felülete mindig azonos hőmérsékletű a levegővel, alső felülete pedig mindig $0\,\mathrm{^\circ C}$-os. A jég olvadáshője $L_o=335\,\mathrm{\frac{J}{g}}$, hővezetési tényezője $\lambda=2,1\cdot10^{-2}\,\mathrm{\frac{J}{s\cdot cm\cdot ^\circ C}}$, sűrűsége pedig $\rho=0,92\,\mathrm{\frac{g}{cm^3}}$.</wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel egy elemi időtartam alatt keletkező elemi vastagságú jégréteg felszabadulásakor keletkező hőt, és tegyük fel, hogy ez a jégrétegen keresztül hővezetéssel távozik, majd integráljuk a kapott egyenletet. Az analitikus megoldás érdekében hanyagoljuk el a jég ''fajhőjét''.}} {{Végeredmény|content=$$ | + | </noinclude><wlatex># Mennyi idő alatt képződik $Z=5\,\mathrm{cm}$ vastag jégréteg egy tó felszínén, ha a léghőmérséklet $T_\ell=-10\,\mathrm{^\circ C}$, a víz hőmérséklete a jégréteg alatt $T_0=0\,\mathrm{^\circ C}$? Tegyük fel, hogy a jégréteg felső felülete mindig azonos hőmérsékletű a levegővel, alső felülete pedig mindig $0\,\mathrm{^\circ C}$-os. A jég olvadáshője $L_o=335\,\mathrm{\frac{J}{g}}$, hővezetési tényezője $\lambda=2{,}1\cdot10^{-2}\,\mathrm{\frac{J}{s\cdot cm\cdot ^\circ C}}$, sűrűsége pedig $\rho=0{,}92\,\mathrm{\frac{g}{cm^3}}$.</wlatex><includeonly><wlatex>{{Útmutatás|content= Írjuk fel egy elemi időtartam alatt keletkező elemi vastagságú jégréteg felszabadulásakor keletkező hőt, és tegyük fel, hogy ez a jégrétegen keresztül hővezetéssel távozik, majd integráljuk a kapott egyenletet. Az analitikus megoldás érdekében hanyagoljuk el a jég ''fajhőjét''.}} {{Végeredmény|content=$$t(Z) = \left(\frac{\rho L_o}{2\lambda(T_0-T_\ell)}\right)\,Z^2, $$ 5 óra alatt képződik $5\,\mathrm{cm}$ vastag jégréteg.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A hővezetés |
$$\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A\frac{\mathrm{d}T}{\mathrm{d}z}$$ | $$\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A\frac{\mathrm{d}T}{\mathrm{d}z}$$ | ||
| − | + | alaptörvényét arra használjuk fel, hogy felírjuk egy már létező $z$ vastagságú jégrétegen keresztüli hőkivonást, ami egy $\mathrm{d}Z$ vastagságú jégréteg megfagyasztásához szükséges. | |
| − | Ha a fagyás kellően lassú, feltehetjük, hogy az [[Termodinamika példák - Lineáris hőmérsékletprofil|előző feladatban]] bizonyított módon lineáris hőmérsékletprofil alakul ki a $Z(t)$ vastag jégrétegben. | + | Ha a fagyás kellően lassú*, feltehetjük, hogy az [[Termodinamika példák - Lineáris hőmérsékletprofil|előző feladatban]] bizonyított módon lineáris hőmérsékletprofil alakul ki a $Z(t)$ vastag jégrétegben. |
$$\frac{dT}{dz}=\frac{T_0-T_\ell}{Z(t)} \qquad \forall z\in(0,Z(t))$$ | $$\frac{dT}{dz}=\frac{T_0-T_\ell}{Z(t)} \qquad \forall z\in(0,Z(t))$$ | ||
| − | A fagyás során vízből $\mathrm{d}z$ vastagságú $\mathrm{d}m$ tömegű $0\,\mathrm{^\circ C}$-os jégréteget | + | A fagyás során vízből $\mathrm{d}z$ vastagságú, $\mathrm{d}m$ tömegű $0\,\mathrm{^\circ C}$-os jégréteget |
| − | $$\mathrm{d}Q= -L_o\mathrm{d}m = -L_o\rho A\mathrm{d}Z$$ | + | $$ \mathrm{d}Q= -L_o\,\mathrm{d}m = -L_o\rho A \,\mathrm{d}Z $$ |
hő elvonásával tudunk létrehozni. | hő elvonásával tudunk létrehozni. | ||
A fenti ismereteket a hővezetési egyenletbe helyettesítve: | A fenti ismereteket a hővezetési egyenletbe helyettesítve: | ||
| − | $$L_o\rho A\frac{\mathrm{d}Z}{\mathrm{d}t}=-\lambda A\frac{T_0-T_\ell}{Z},$$ | + | $$ L_o \rho A \frac{\mathrm{d}Z}{\mathrm{d}t} = -\lambda A \frac{T_0-T_\ell}{Z}, $$ |
| − | amit a változók szétválasztásának módszerével megoldhatunk, | + | amit a változók szétválasztásának módszerével megoldhatunk, |
| − | $$Z(t)=\left(\frac{2\lambda(T_0-T_\ell)}{\rho L_o}\right)^{1/2}t^{1/2},$$ | + | $$ Z(t) = \left(\frac{2\lambda(T_0-T_\ell)}{\rho L_o}\right)^{1/2}t^{1/2}, $$ |
| + | $$ t(Z) = \left(\frac{\rho L_o}{2\lambda(T_0-T_\ell)}\right)\,Z^2, $$ | ||
azaz 5 óra alatt képződik $5\,\mathrm{cm}$ vastag jégréteg. | azaz 5 óra alatt képződik $5\,\mathrm{cm}$ vastag jégréteg. | ||
== Megjegyzés == | == Megjegyzés == | ||
| − | A feladatot nagyon elbonyolítaná, ha figyelembe akarnánk venni, hogy a már meglevő jégrétegben fenn kell tartanunk a lineáris hőmérsékletprofilt és ez további (helyfüggő nagyságú) hőáramot igényel. Ez a közelítés $L_0 \gg c\cdot 10\,\mathrm{^\circ C}=20,93\,\mathrm{\frac{J}{g}}$ miatt indokolt nem túl vastag jégpáncélra. | + | <nowiki>*</nowiki> A feladatot nagyon elbonyolítaná, ha figyelembe akarnánk venni, hogy a már meglevő jégrétegben fenn kell tartanunk a lineáris hőmérsékletprofilt és ez további (helyfüggő nagyságú) hőáramot igényel. Ez a közelítés $L_0 \gg c\cdot 10\,\mathrm{^\circ C}=20{,}93\,\mathrm{\frac{J}{g}}$ miatt indokolt nem túl vastag jégpáncélra. |
| − | + | A valóságban a hőmérsékletprofil változását is figyelembe vevő $\frac{\partial T}{\partial t} = -\frac{\lambda}{c\rho} \frac{\partial^2 T}{\partial z^2}$ nem stacionárius hővezetési egyenletet az előbbi, fagyást leíró egyenlettel együtt $T(z=0,t)=-10\,\mathrm{^\circ C}$ és $T(z=Z(t),t)=0\,\mathrm{^\circ C}$ mozgó peremfeltétel mellett kellene megoldani, ahol $T(z,t)$ és $Z(t)$ is ismeretlen. | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. június 13., 22:11-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Mennyi idő alatt képződik
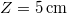vastag jégréteg egy tó felszínén, ha a léghőmérséklet 
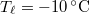, a víz hőmérséklete a jégréteg alatt 
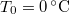? Tegyük fel, hogy a jégréteg felső felülete mindig azonos hőmérsékletű a levegővel, alső felülete pedig mindig 
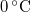-os. A jég olvadáshője 
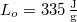, hővezetési tényezője 
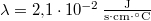, sűrűsége pedig 
.
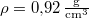Megoldás
A hővezetés
![\[\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A\frac{\mathrm{d}T}{\mathrm{d}z}\]](/images/math/4/4/1/44168ec8fab4aa12ba618956be4ca6f4.png)
alaptörvényét arra használjuk fel, hogy felírjuk egy már létező 
vastagságú jégrétegen keresztüli hőkivonást, ami egy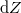 
vastagságú jégréteg megfagyasztásához szükséges.
Ha a fagyás kellően lassú*, feltehetjük, hogy az előző feladatban bizonyított módon lineáris hőmérsékletprofil alakul ki a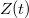 
vastag jégrétegben.
![\[\frac{dT}{dz}=\frac{T_0-T_\ell}{Z(t)} \qquad \forall z\in(0,Z(t))\]](/images/math/b/4/1/b41a8f0921d714bde9b20663b4692563.png)
A fagyás során vízből 
vastagságú,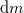 
tömegű 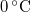-os jégréteget
![\[ \mathrm{d}Q= -L_o\,\mathrm{d}m = -L_o\rho A \,\mathrm{d}Z \]](/images/math/7/8/4/784c9dbfa2cef7d651bbcdececaf2a1a.png)
hő elvonásával tudunk létrehozni.
A fenti ismereteket a hővezetési egyenletbe helyettesítve:
![\[ L_o \rho A \frac{\mathrm{d}Z}{\mathrm{d}t} = -\lambda A \frac{T_0-T_\ell}{Z}, \]](/images/math/2/4/2/242d431d52d6f8065dbebaaca41c95ef.png)
amit a változók szétválasztásának módszerével megoldhatunk,
![\[ Z(t) = \left(\frac{2\lambda(T_0-T_\ell)}{\rho L_o}\right)^{1/2}t^{1/2}, \]](/images/math/3/d/1/3d12a0017830a6923453ccb6a8da5b5d.png)
![\[ t(Z) = \left(\frac{\rho L_o}{2\lambda(T_0-T_\ell)}\right)\,Z^2, \]](/images/math/d/9/c/d9cd81a16c066703ec4b2e038d500da4.png)
azaz 5 óra alatt képződik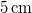 
vastag jégréteg.
Megjegyzés
* A feladatot nagyon elbonyolítaná, ha figyelembe akarnánk venni, hogy a már meglevő jégrétegben fenn kell tartanunk a lineáris hőmérsékletprofilt és ez további (helyfüggő nagyságú) hőáramot igényel. Ez a közelítés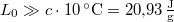 
miatt indokolt nem túl vastag jégpáncélra.
A valóságban a hőmérsékletprofil változását is figyelembe vevő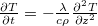 
nem stacionárius hővezetési egyenletet az előbbi, fagyást leíró egyenlettel együtt 
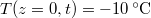és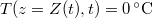 
mozgó peremfeltétel mellett kellene megoldani, ahol 
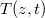és 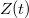is ismeretlen.
