„Termodinamika példák - Telített vízgőz dugattyúban” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Fázisátalakulások {{Kísérleti fizika g…”) |
a (Szöveg koherenssé tétele) |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Henger alakú edényben $T_f=100\,\mathrm{\,^\circ C}$ hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben $\Delta m=0{,}7\mathrm{g}$ víz lecsapódik. A víz moláris tömege $18{,}01528\mathrm{\frac{g}{mol}}$ A folyamat során a nyomás a $p_k$ külső légnyomással egyenlő.<br />Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta W=p_k\left(V_1-V_2\right)=\frac{RT_f}{M}\Delta m=120\,\mathrm{J}$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># Henger alakú edényben $T_f=100\,\mathrm{\,^\circ C}$ hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben $\Delta m=0{,}7\,\mathrm{g}$ víz lecsapódik. A víz moláris tömege $18{,}01528\mathrm{\frac{g}{mol}}$ A folyamat során a nyomás a $p_k$ külső légnyomással egyenlő.<br />Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta W=p_k\left(V_1-V_2\right)=\frac{RT_f}{M}\Delta m=120\,\mathrm{J}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Az összenyomás hatására a víz és a telített gőz aránya változik meg a dugattyúban, a nyomás végig a $100\,\mathrm{^\circ C}$-os telített vízgőz nyomásával (légköri nyomással) egyenlő. A gőz halmazállapotú részrendszer állapotegyenlete a két állapotban: |
| + | $$ \frac{m_1} MR T_f = p_k V_1 \qquad\text{és}\qquad \frac{m_2} MR T_f = p_k V_2. $$ | ||
| + | |||
| + | A végzett mechanikai munkát kifejezhetjük a megadott adatokkal: | ||
| + | $$ \Delta W = p_k \Delta V | ||
| + | = p_k\left(V_2-V_1\right) | ||
| + | = \frac{m_2-m_1}{M} R T_f | ||
| + | \approx 120{,}4\,\mathrm{J}. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 24., 19:10-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Henger alakú edényben
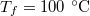hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben 
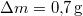víz lecsapódik. A víz moláris tömege 
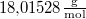A folyamat során a nyomás a 
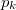külső légnyomással egyenlő.
Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?
Megoldás
Az összenyomás hatására a víz és a telített gőz aránya változik meg a dugattyúban, a nyomás végig a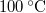 
-os telített vízgőz nyomásával (légköri nyomással) egyenlő. A gőz halmazállapotú részrendszer állapotegyenlete a két állapotban:
![\[ \frac{m_1} MR T_f = p_k V_1 \qquad\text{és}\qquad \frac{m_2} MR T_f = p_k V_2. \]](/images/math/f/1/4/f1484c9136cd91891c7cb9323182ee64.png)
A végzett mechanikai munkát kifejezhetjük a megadott adatokkal:
![\[ \Delta W = p_k \Delta V = p_k\left(V_2-V_1\right) = \frac{m_2-m_1}{M} R T_f \approx 120{,}4\,\mathrm{J}. \]](/images/math/a/e/c/aecb6d1ff30f084a9c6ff3f7fb25d36b.png)
