„Termodinamika példák - Jég olvadáshőjének becslése” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Fázisátalakulások {{Kísérleti fizika g…”) |
a (Jelölések egységesítése) |
||
| (egy szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># A jég olvadáshője $1\,\mathrm{bar}$ nyomáson$L=335\,\mathrm{\frac{kJ}{kg}}$. A jég és a víz fajlagos térfogatának aránya $1{,}09:1{,}00$. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\mathrm{d}T=-\frac{0{,} | + | </noinclude><wlatex># A jég olvadáshője $1\,\mathrm{bar}$ nyomáson $L=335\,\mathrm{\frac{kJ}{kg}}$. A jég és a víz fajlagos térfogatának aránya $1{,}09:1{,}00$. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\mathrm{d}T=-\frac{0{,}09v_\text{víz}T}{L}\,\mathrm{d}p= -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Alkalmazzuk a ''Clapeyron''-egyenlet |
| + | $$ \mathrm{d}T = \frac{T\Delta V_M}{L_M}\,\mathrm{d}p $$ | ||
| + | alakját az olvadásra. Tudjuk, hogy | ||
| + | $$ \frac{\Delta V_M^\text{olv}}{L_M^\text{olv}} = \frac{\Delta v_\text{olv}}{L_\text{olv}}, $$ | ||
| + | hiszen a moláris mennyiségeket egységnyi tömegre bővíthetjük. A fázisátalakulásban a jeget tekintjük kezdeti, a vizet végállapotnak ($T_\text{olv} \Delta S_\text{olv} = L_\text{olv} > 0$): | ||
| + | $$ \Delta v_\text{olv} = (1{,}00-1{,}09) v_\text{víz}, $$ | ||
| + | hiszen a víz $v_\text{víz} = 0{,}001\,\mathrm{\frac{m^3}{kg}}$ fajlagos térfogatát adták meg referenciaként. A jég olvadáshője $L_\text{olv} =335\,\mathrm{\frac{kJ}{kg}}$, olvadáspontja $T_\text{olv}=273{,}15\,\mathrm{K}$, amivel | ||
| + | $$ \mathrm{d}T = -\frac{0{,}09v_\text{víz}T_\text{olv}}{L_\text{olv}}\,\mathrm{d}p | ||
| + | = -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p. $$ | ||
| + | |||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 28., 21:54-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- A jég olvadáshője
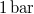nyomáson 
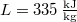. A jég és a víz fajlagos térfogatának aránya 
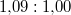. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
Megoldás
Alkalmazzuk a Clapeyron-egyenlet
![\[ \mathrm{d}T = \frac{T\Delta V_M}{L_M}\,\mathrm{d}p \]](/images/math/1/c/9/1c9a928d4df240fee8dd8ba16af94782.png)
alakját az olvadásra. Tudjuk, hogy
![\[ \frac{\Delta V_M^\text{olv}}{L_M^\text{olv}} = \frac{\Delta v_\text{olv}}{L_\text{olv}}, \]](/images/math/5/c/e/5ce586dfb4c02b016bc88afea36eb6c0.png)
hiszen a moláris mennyiségeket egységnyi tömegre bővíthetjük. A fázisátalakulásban a jeget tekintjük kezdeti, a vizet végállapotnak (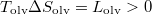
):
![\[ \Delta v_\text{olv} = (1{,}00-1{,}09) v_\text{víz}, \]](/images/math/e/5/5/e55a7a88c0b683ae09bb90a5948ceb63.png)
hiszen a víz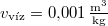 
fajlagos térfogatát adták meg referenciaként. A jég olvadáshője 
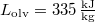, olvadáspontja 
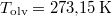, amivel
![\[ \mathrm{d}T = -\frac{0{,}09v_\text{víz}T_\text{olv}}{L_\text{olv}}\,\mathrm{d}p = -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p. \]](/images/math/2/8/5/285302e1fd5d53432663024f5c7d6639.png)
