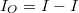„Magnetosztatika példák - Koaxiális vezető mágneses tere” változatai közötti eltérés
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#Az ábrán látható koaxiális vezetőben $I$ áram folyik. A belső éren ($a$-n belül) befelé, a külső éren ($b$ és $c$ között) kifelé. Határozzuk meg a mágneses teret a tengelytől mért $r$ távolság függvényében. </wlatex><includeonly><wlatex>{{Végeredmény|content= A belső hengerben a térerősség helyfüggése: $$H=\dfrac{I}{2\pi a^2} r$$ A két henger között ($a<r<b$):$$H=\dfrac{I}{2\pi r}$$ A térerősség a külső hengerben | + | </noinclude><wlatex>#Az ábrán látható koaxiális vezetőben $I$ áram folyik. A belső éren ($a$-n belül) befelé, a külső éren ($b$ és $c$ között) kifelé. Határozzuk meg a mágneses teret a tengelytől mért $r$ távolság függvényében. </wlatex><includeonly><wlatex>{{Végeredmény|content= A belső hengerben ($r<a$) a térerősség helyfüggése: $$H=\dfrac{I}{2\pi a^2} r$$ A két henger között ($a<r<b$):$$H=\dfrac{I}{2\pi r}$$ A térerősség a külső hengerben ($b<r<c$): $$H=\dfrac{I}{2\pi r}\dfrac{c^2-r^2}{c^2-b^2}$$ A két hengeren kívüli térben ($c<r$) a térerősség zérus}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
A lap 2013. július 14., 19:17-kori változata
Feladat
- Az ábrán látható koaxiális vezetőben
áram folyik. A belső éren (
-n belül) befelé, a külső éren (
és 
között) kifelé. Határozzuk meg a mágneses teret a tengelytől mért 
távolság függvényében.
Megoldás
Mivel a rendszer teljesen hengerszimmetrikus, könnyen alkalmazhatjuk az Amper-féle gerjesztési törvényt.
![\[I=\oint \vec{H}\vec{dl}\]](/images/math/f/7/f/f7fef70eec61dbd4f6e4de4e63bc5f52.png)
Vegyünk fel egy sugarú gyűrűt, mint zárt görbét, melynek tengelye egybeesik a hengerek tengelyével. A rendszer hengerszimmetrikus, így joggal feltételezzük, hogy a 
térerősség nagysága a gyűrű minden pontján azonos nagyságú, iránya pedig mindenütt érintő irányú. A vektorok skalárszorzatának integrálja így a következőképp egyszerűsíthető:
![\[I_O=2r\pi H\]](/images/math/7/4/1/741cc5c10b3b2d8250c91f265a467002.png)
![\[H=\dfrac{I_O}{2\pi r}\]](/images/math/a/0/d/a0d68e769cd7a4506cbc33ea4471e32f.png)
Ahol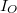 
a gyűrű által határolt területen átfolyó áram erőssége. Ha 
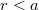, a gyűrűn átfolyó áram erőssége arányos az sugarú hengerben folyó árammal, az arányossági tényező pedig a gyűrű területének és a henger keresztmetszetének hányadosa:
![\[I_O=I\dfrac{r^2}{a^2}\]](/images/math/d/8/a/d8a8a7cce183742d7fa18a4b696218b9.png)
Tehát a belső hengerben a térerősség helyfüggése:
![\[H=\dfrac{I}{2\pi a^2} r\]](/images/math/4/5/a/45ac1ecfbedc24d0d14c4c6f28abea7b.png)
A két henger között (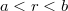
) az Amper-féle gerjesztési törvény a fentiekhez hasonlóan alkalmazható, ám a zárt gyűrűn átfolyó összes áram megegyezik a belső hengerben folyó árammal, tehát a mágneses tér helyfüggése:
![\[H=\dfrac{I}{2\pi r}\]](/images/math/9/7/e/97e37ebdd4fa3accb5b02fb8864c462e.png)
Tovább növelve az Amper-törvény zárt görbéjének sugarát (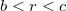
) a zárt görbe által határolt területen átfolyó összes áram erőssége csökken, hiszen a külső hengerben folyó, belsővel ellentétes irányú áram egy részét is bezárja. A területek arányainak ismeretében meghatározható a zárt görbe által határolt áramok nagysága:
![\[I_O=I-I\dfrac{r^2-b^2}{c^2-b^2}=I \left( \dfrac{c^2-r^2}{c^2-b^2} \right)\]](/images/math/1/f/1/1f1184ab64b10aaa87f6ff5a55eeb66d.png)
A térerősség a külső hengerben tehát:
![\[H=\dfrac{I}{2\pi r}\dfrac{c^2-r^2}{c^2-b^2}\]](/images/math/e/a/4/ea49738098a748261ba8db7bd7b31436.png)
A két hengeren kívüli térben (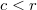
) a térerősség zérus, hiszen az 
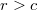sugarú zárt görbe által határolt felületen egyaránt átfolyik a belső henger árama, és a külső henger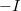 
erősségű árama. Ezek összege pedig nulla: 
