„Magnetosztatika példák - Forgó korong mágneses tere” változatai közötti eltérés
(→Megoldás) |
|||
| 11. sor: | 11. sor: | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | A forgó korong a [[Magnetosztatika példák - Körmozgást végző töltött test mágneses tere|Körmozgást végző töltött test mágneses tere]] feladatához hasonló megfontolások alapján köráramok sokaságaként írható fel. Az $R$ sugarú korongot felosztjuk $dr$ szélességű, $r$ sugarú gyűrűkre, és meghatározzuk, hogy az egyes gyűrűk mekkora köráramnak felelnek meg. A köráram mágneses terét annak tengelyén már meghatároztuk a [[Magnetosztatika példák - Körmozgást végző töltött test mágneses tere|Körmozgást végző töltött test mágneses tere]] feladatában, feladatunk tehát csak ezen elemi köráramok felösszegzése a korong teljes felületén. | + | A forgó korong a [[Magnetosztatika példák - Körmozgást végző töltött test mágneses tere|Körmozgást végző töltött test mágneses tere]] feladatához hasonló megfontolások alapján köráramok sokaságaként írható fel. Az $R$ sugarú korongot felosztjuk $dr$ szélességű, $r$ sugarú gyűrűkre, és meghatározzuk, hogy az egyes gyűrűk mekkora köráramnak felelnek meg. A köráram mágneses terét annak tengelyén már meghatároztuk a [[Magnetosztatika példák - Körmozgást végző töltött test mágneses tere|Körmozgást végző töltött test mágneses tere]] feladatában, feladatunk tehát csak ezen elemi köráramok indukció járulékainak felösszegzése a korong teljes felületén. |
Az $r$ sugarú, $dr$ szélességű elemi gyűrű $dq$ töltése: | Az $r$ sugarú, $dr$ szélességű elemi gyűrű $dq$ töltése: | ||
A lap jelenlegi, 2013. szeptember 14., 21:11-kori változata
Feladat
- Egy R sugarú üvegkorong egyik oldalát
egyenletes töltéssűrűséggel látjuk el. A korongot a szimmetriatengelye körül 
szögsebességgel megforgatjuk. Mekkora lesz a mágneses tér a korong tengelyén, a korong síkjától 
távolságban?
Megoldás
A forgó korong a Körmozgást végző töltött test mágneses tere feladatához hasonló megfontolások alapján köráramok sokaságaként írható fel. Az 
sugarú korongot felosztjuk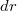 
szélességű, 
sugarú gyűrűkre, és meghatározzuk, hogy az egyes gyűrűk mekkora köráramnak felelnek meg. A köráram mágneses terét annak tengelyén már meghatároztuk a Körmozgást végző töltött test mágneses tere feladatában, feladatunk tehát csak ezen elemi köráramok indukció járulékainak felösszegzése a korong teljes felületén.
Az sugarú, 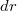szélességű elemi gyűrű 
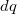töltése:
![\[dq=2\pi r\Omega dr\]](/images/math/9/4/7/94719c56b90902fac61f4abfddc9d853.png)
Az szögsebességgel keringő elemi 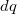töltés 
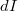erősségű köráramnak felel meg:
![\[dI=\dfrac{dq\omega}{2\pi}=\Omega \omega r dr\]](/images/math/4/9/2/492d844bec953a99f75efdd741e93201.png)
Ezen kicsiny köráramnak pontban keltett mágneses tere a 6. feladatsor 11. feladatának eredményét felhasználva:
![\[dB_z=\dfrac{\mu_0 dI r^2}{2 (r^2+z^2)^{3/2}}\]](/images/math/7/a/e/7aea7ccdcd082d6979c6d8795910f7d5.png)
A fenti kifejezésbe beírva az infinitezimális áramra kapott összefüggést:
![\[dB_z=\dfrac{\mu_0 \Omega \omega r^3}{2 (r^2+z^2)^{3/2}}dr\]](/images/math/9/a/e/9aefc06243926acffe69e39167edaf76.png)
A teljes korong által keltett teret megkaphatjuk, ha az elemi köráramok indukció-járulékát felösszegezzük a korong közepétől a pereméig:
![\[B_z=\int dB_z=\dfrac{\mu_0 \Omega \omega}{2} \int_0^R \dfrac{r^3}{ (r^2+z^2)^{3/2}}dr\]](/images/math/a/4/7/a4761ddb97a546382f87e224d68fcdbf.png)
Az integrálást elvégezve:
![\[B_z=\dfrac{\mu_0 \Omega \omega}{2} \left[ \dfrac{r^2+2z^2}{ (r^2+z^2)^{1/2}} \right]_0^R= \dfrac{\mu_0 \Omega \omega}{2} \left( \dfrac{R^2+2z^2}{ (R^2+z^2)^{1/2}} -2z\right)\]](/images/math/f/8/b/f8b72aadb1a696cc9f2c390167ab863a.png)
