„Termodinamika példák - Lineáris hőmérsékletprofil” változatai közötti eltérés
A Fizipedia wikiből
| 16. sor: | 16. sor: | ||
</noinclude><wlatex># Egy $d$ vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó $T_1$ és $T_2$, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért $x$ távolsággal, és írjuk fel a $T(x)$ függvényt a megadott mennyiségekkel!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T(x)=T_1+\frac{T_2-T_1}{d}x$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># Egy $d$ vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó $T_1$ és $T_2$, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért $x$ távolsággal, és írjuk fel a $T(x)$ függvényt a megadott mennyiségekkel!</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T(x)=T_1+\frac{T_2-T_1}{d}x$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A $j_z=-\lambda \frac{\mathrm{d}T}{\mathrm{d}z}$ hőáramra felírt egyenletet vonatkoztassuk most egy rögzített $A$ keresztmetszetre: $J_Q=\frac{\mathrm{d}Q}{\mathrm{d}t}$ átadott hőteljesítményt kapjuk: |
| + | $$\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}$$ | ||
| + | |||
| + | Mivel stacionárius esetben hő nem halmozódhat fel, $J_Q$ állandó minden $A$ nagyságú keresztmetszetre, bármely $z$ magasságban legyen is az. | ||
| + | |||
| + | Ebből viszont következik, hogy $\frac{\mathrm{d}T}{\mathrm{d}z}$ állandó, aminek megoldása $T(z) = T_0 + c_T z$ lineáris függvény. | ||
| + | |||
| + | A peremfeltételekre illesztve $$T(z)=\frac{T_1-T_2}{d}z + T_ 2$$ | ||
| + | adódik. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 3., 12:55-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó 
és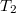 
, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért 
távolsággal, és írjuk fel a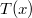 
függvényt a megadott mennyiségekkel!
Megoldás
A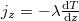 
hőáramra felírt egyenletet vonatkoztassuk most egy rögzített 
keresztmetszetre: 
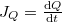átadott hőteljesítményt kapjuk:
![\[\frac{\mathrm{d}Q}{\mathrm{d}t}=-\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}\]](/images/math/8/d/6/8d63ae626886927c432ec742b94398be.png)
Mivel stacionárius esetben hő nem halmozódhat fel,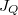 
állandó minden nagyságú keresztmetszetre, bármely 
magasságban legyen is az.
Ebből viszont következik, hogy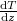 
állandó, aminek megoldása 
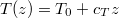lineáris függvény.
![\[T(z)=\frac{T_1-T_2}{d}z + T_ 2\]](/images/math/6/2/d/62da0de01e5bde727c783d1a3eb48e15.png)
adódik.
