„Termodinamika példák - Hővezetés” változatai közötti eltérés
A Fizipedia wikiből
| 15. sor: | 15. sor: | ||
</noinclude><wlatex># $T_0$ hőmérsékletű, igen nagy hőkapacitású folyadékba $T_1>T_0$ hőmérsékletű, $m$ tömegű és $c$ fajhőjű, abszolút jó hővezető testet helyezünk a $t=0$ pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik ($\text{hőáramsűrűség}=\alpha(T-T_0)$), az $\alpha$ hőátadási tényező ismert, a test felületének nagysága $A$. Határozzuk meg a test hőmérsékletét $t$ idő eltelte után!</wlatex><includeonly><wlatex>{{{Útmutatás|content=A leadott hőt fejezzük ki egyrészt a hőkapacitással, és a hőmérsékletváltozással, másrészt a folyadékba történő hőátadással, és integráljuk a kapott egyenletet.}} {{Végeredmény|content=$$T=T_0+(T_1-T_0)\exp\{-\frac{\alpha A}{mc}t\}$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># $T_0$ hőmérsékletű, igen nagy hőkapacitású folyadékba $T_1>T_0$ hőmérsékletű, $m$ tömegű és $c$ fajhőjű, abszolút jó hővezető testet helyezünk a $t=0$ pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik ($\text{hőáramsűrűség}=\alpha(T-T_0)$), az $\alpha$ hőátadási tényező ismert, a test felületének nagysága $A$. Határozzuk meg a test hőmérsékletét $t$ idő eltelte után!</wlatex><includeonly><wlatex>{{{Útmutatás|content=A leadott hőt fejezzük ki egyrészt a hőkapacitással, és a hőmérsékletváltozással, másrészt a folyadékba történő hőátadással, és integráljuk a kapott egyenletet.}} {{Végeredmény|content=$$T=T_0+(T_1-T_0)\exp\{-\frac{\alpha A}{mc}t\}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Hővezetés alapegyenlete a Newton-féle lehűlési törvénnyel: |
| + | $$\frac{\mathrm{d}Q}{\mathrm{d}t}=A\alpha \left(T-T_0\right)$$ | ||
| + | |||
| + | A test hűlését jellemző $\mathrm{d}Q=-cm\mathrm{d}T$ kifejezést behelyettesítve kapott differenciálegyenlet a változók szétválasztásának módszerével megoldható | ||
| + | $$-\frac{cm\mathrm{d}T}{\mathrm{d}t}=A\alpha \left(T-T_0\right),$$ | ||
| + | az eredmény akezdeti feltételeket is figyelembe véve ($T(0)=T_1$) | ||
| + | $$\ln \left(\frac{T-T_0}{T_1-T_0}\right)=\frac{A\alpha}{cm}t.$$ | ||
| + | |||
| + | Ebből a test pillanatnyi hőmérséklete: | ||
| + | $$T= T_0+\left(T_1-T_0\right)e^{\displaystyle -\frac{A\alpha}{cm}t}.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 3., 21:58-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
 hőmérsékletű, igen nagy hőkapacitású folyadékba
hőmérsékletű, igen nagy hőkapacitású folyadékba 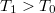 hőmérsékletű,
hőmérsékletű,  tömegű és
tömegű és  fajhőjű, abszolút jó hővezető testet helyezünk a
fajhőjű, abszolút jó hővezető testet helyezünk a  pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik (
pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik (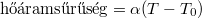 ), az
), az  hőátadási tényező ismert, a test felületének nagysága
hőátadási tényező ismert, a test felületének nagysága  . Határozzuk meg a test hőmérsékletét
. Határozzuk meg a test hőmérsékletét  idő eltelte után!
idő eltelte után!
Megoldás
Hővezetés alapegyenlete a Newton-féle lehűlési törvénnyel:
![\[\frac{\mathrm{d}Q}{\mathrm{d}t}=A\alpha \left(T-T_0\right)\]](/images/math/3/5/2/352b7a3a979dab302be1837b260b19a5.png)
A test hűlését jellemző 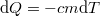 kifejezést behelyettesítve kapott differenciálegyenlet a változók szétválasztásának módszerével megoldható
kifejezést behelyettesítve kapott differenciálegyenlet a változók szétválasztásának módszerével megoldható
![\[-\frac{cm\mathrm{d}T}{\mathrm{d}t}=A\alpha \left(T-T_0\right),\]](/images/math/4/b/d/4bdd39ddbae6471566882127af16d688.png)
az eredmény akezdeti feltételeket is figyelembe véve (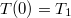 )
)
![\[\ln \left(\frac{T-T_0}{T_1-T_0}\right)=\frac{A\alpha}{cm}t.\]](/images/math/2/4/1/24180fc1632a95d38cd01974c22046dc.png)
Ebből a test pillanatnyi hőmérséklete:
![\[T= T_0+\left(T_1-T_0\right)e^{\displaystyle -\frac{A\alpha}{cm}t}.\]](/images/math/b/4/5/b45f108893b79d14cb238da56e5acfec.png)