„Termodinamika példák - Ideális gáz állapotváltozása egyenlettel” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 20. sor: | 20. sor: | ||
Az ideális gázra speciálisan a belső energia térfogat szerinti parciális deriváltja nulla. A térfogat infinitezimális megváltozását a folyamatot jellemző úton kifejezhetjük a hőmérséklettel: | Az ideális gázra speciálisan a belső energia térfogat szerinti parciális deriváltja nulla. A térfogat infinitezimális megváltozását a folyamatot jellemző úton kifejezhetjük a hőmérséklettel: | ||
$$C n \mathrm{d}T = C_V n \mathrm{d}T+ | $$C n \mathrm{d}T = C_V n \mathrm{d}T+ | ||
| − | p\left(\frac{\mathrm{d} V}{\mathrm{d} T}\right)_{\text{ | + | p\left(\frac{\mathrm{d} V}{\mathrm{d} T}\right)_{\substack{\text{állapot-}\\ \text{változás}}}\mathrm{d}T.$$ |
Az ideális gáz $pV=nRT$ állapotegyenletéből és a folyamatot jellemző $p=\frac{k^2}{V^2}$ egyenletből a térfogat és a folyamatot jellemző deriváltja számítható: | Az ideális gáz $pV=nRT$ állapotegyenletéből és a folyamatot jellemző $p=\frac{k^2}{V^2}$ egyenletből a térfogat és a folyamatot jellemző deriváltja számítható: | ||
| − | $$V=\frac{k^2}{nRT}\qquad\text{és}\qquad\frac{\mathrm{d}V}{\mathrm{d}T}=-\frac{k^2}{nRT^2}$$ | + | $$V=\frac{k^2}{nRT}\qquad\text{és}\qquad\frac{\mathrm{d}V}{\mathrm{d}T}=-\frac{k^2}{nRT^2}=-\frac{V}{T}$$ |
Ezt visszaírva a folyamatot jellemző $C$ fajhő kifejezésébe azt kapjuk, hogy | Ezt visszaírva a folyamatot jellemző $C$ fajhő kifejezésébe azt kapjuk, hogy | ||
| + | $$C n \mathrm{d}T = (C_V n - \frac{pV}{T})\mathrm{d}T = (C_V n - nR)\mathrm{d}T,$$ | ||
| + | ahonnan a fajhő leolvasható: | ||
| + | $$ C = C - n. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2012. október 9., 20:08-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Melegszik vagy lehűl az
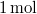ideális gáz, ha a 
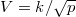összefüggés (
állandó) szerint tágul ki? Mekkora a gáz mólhője ebben a folyamatban, ha állandó térfogaton mért mólhője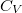 
?
Megoldás
A termodinamika első főtétele szerint![\[\delta Q = \mathrm{d}U+p\,\mathrm{d}V,\]](/images/math/0/9/6/09608eb0a969432fd57642dcb7e8070c.png)
ahol a belső energiát a hőmérséklet és a térfogat függvényeként fogjuk fel (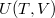
), ezzel:
![\[\delta Q = \left(\frac{\partial U}{\partial T}\right)_V\mathrm{d}T+ \left(\frac{\partial U}{\partial V}\right)_T\mathrm{d}V+ p\,\mathrm{d}V.\]](/images/math/4/5/7/4576af24ab8b23a9bf31e1fa445b3d68.png)
Az utolsó két tag sorrendjét felcserélve általánosan levezethető, hogy
![\[C n \mathrm{d}T = C_V n \mathrm{d}T+ \left[p+\frac{\partial U}{\partial V}\right]_T\mathrm{d}V.\]](/images/math/5/2/1/521ec92a9c0043e71e15664a892e20cb.png)
Az ideális gázra speciálisan a belső energia térfogat szerinti parciális deriváltja nulla. A térfogat infinitezimális megváltozását a folyamatot jellemző úton kifejezhetjük a hőmérséklettel:
![\[C n \mathrm{d}T = C_V n \mathrm{d}T+ p\left(\frac{\mathrm{d} V}{\mathrm{d} T}\right)_{\substack{\text{állapot-}\\ \text{változás}}}\mathrm{d}T.\]](/images/math/3/7/c/37cddea6d509732458ce859577c71561.png)
Az ideális gáz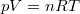 
állapotegyenletéből és a folyamatot jellemző 
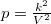egyenletből a térfogat és a folyamatot jellemző deriváltja számítható:
![\[V=\frac{k^2}{nRT}\qquad\text{és}\qquad\frac{\mathrm{d}V}{\mathrm{d}T}=-\frac{k^2}{nRT^2}=-\frac{V}{T}\]](/images/math/e/6/a/e6abcf24148c972832e6490cdf6a30c3.png)
Ezt visszaírva a folyamatot jellemző 
fajhő kifejezésébe azt kapjuk, hogy
![\[C n \mathrm{d}T = (C_V n - \frac{pV}{T})\mathrm{d}T = (C_V n - nR)\mathrm{d}T,\]](/images/math/5/8/b/58b65c11ddb789e86b51a50bcb044378.png)
ahonnan a fajhő leolvasható:
![\[ C = C - n. \]](/images/math/e/7/2/e721787206d63d6bca1c5913c8b34e5a.png)
