„Termodinamika példák - Energiaváltozások diagramból” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
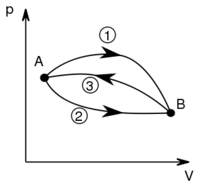
| − | </noinclude><wlatex># Ha egy rendszert az ábrán látható 1 úton viszünk az $A$ állapotból a $B$ állapotba, $100\,\rm{J}$ hőt vesz fel, miközben $30\,\rm{J}$ munkát végez.</wlatex> | + | </noinclude><wlatex># Ha egy rendszert az ábrán látható 1 úton viszünk az $A$ állapotból a $B$ állapotba, $100\,\rm{J}$ hőt vesz fel, miközben $30\,\rm{J}$ munkát végez.[[Fájl:Három útvonal p-V diagramban.svg|thumb|none|200px]]</wlatex> |
#* a) <wlatex>Mennyi hőt vesz fel a rendszer az $A$ és $B$ állapotok közt a 2 úton, ha közben $10\,\rm{J}$ munkát végez?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta Q = 80\,\rm{J}$$}}</wlatex></includeonly> | #* a) <wlatex>Mennyi hőt vesz fel a rendszer az $A$ és $B$ állapotok közt a 2 úton, ha közben $10\,\rm{J}$ munkát végez?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta Q = 80\,\rm{J}$$}}</wlatex></includeonly> | ||
#* b) <wlatex>Ha $20\,\rm{J}$ munkával vihetjük a rendszert $B$-ből $A$-ba a 3 út mentén, mennyi a közben leadott hő?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta Q = 90\,\rm{J}$$}}</wlatex></includeonly><noinclude> | #* b) <wlatex>Ha $20\,\rm{J}$ munkával vihetjük a rendszert $B$-ből $A$-ba a 3 út mentén, mennyi a közben leadott hő?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\Delta Q = 90\,\rm{J}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A táblázat kék cellái adottak, a számítás során az első főtételt ($\Delta U = \Delta Q + \Delta W$) alkalmazzuk, illetve, hogy a belső energia megváltozása az $A$ és $B$ pont között független az útvonaltól. A harmadik útvonalnál belső energia megváltozása ellentettjének vételével vesszük figyelembe az ellentétes irányítást. |
| + | {| style="padding: 10px; min-width: 25%; min-height: 20%; margin-left: auto; margin-right:auto; text-align: center;" | ||
| + | ! | ||
| + | ! {{Hl1}} | Δ''Q'' | ||
| + | ! {{Hl1}} | Δ''W'' | ||
| + | ! {{Hl1}} | Δ''U'' | ||
| + | |- | ||
| + | ! {{Hl1}} | 1 | ||
| + | | {{Hl2}} | 100 J | ||
| + | | {{Hl2}} | 30 J | ||
| + | | 70 J | ||
| + | |- | ||
| + | ! {{Hl1}} | 2 | ||
| + | | 80 J | ||
| + | | {{Hl2}} | 10 J | ||
| + | | 70 J | ||
| + | |- | ||
| + | ! {{Hl1}} | 3 | ||
| + | | -90 J | ||
| + | | {{Hl2}} | -20 J | ||
| + | | -70 J | ||
| + | |} | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 6., 18:27-kori változata
Feladat
- Ha egy rendszert az ábrán látható 1 úton viszünk az
állapotból a 
állapotba, 
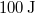hőt vesz fel, miközben 
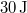munkát végez.
- a) Mennyi hőt vesz fel a rendszer az és állapotok közt a 2 úton, ha közben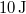
munkát végez?
- b) Ha
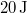munkával vihetjük a rendszert -ből -ba a 3 út mentén, mennyi a közben leadott hő?
- a) Mennyi hőt vesz fel a rendszer az
Megoldás
A táblázat kék cellái adottak, a számítás során az első főtételt (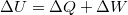
) alkalmazzuk, illetve, hogy a belső energia megváltozása az és pont között független az útvonaltól. A harmadik útvonalnál belső energia megváltozása ellentettjének vételével vesszük figyelembe az ellentétes irányítást.
| ΔQ | ΔW | ΔU | |
|---|---|---|---|
| 1 | 100 J | 30 J | 70 J |
| 2 | 80 J | 10 J | 70 J |
| 3 | -90 J | -20 J | -70 J |
