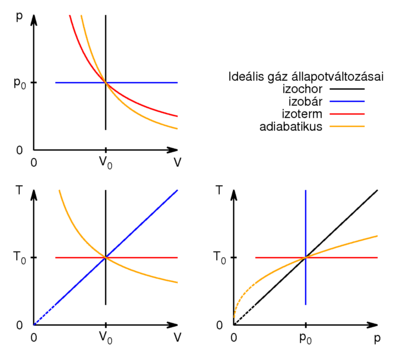„Termodinamika példák - Állapotváltozások diagramjai” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 16. sor: | 16. sor: | ||
#: állapotváltozásáról $p-V$, $T-V$ és $T-p$ koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!</wlatex><noinclude> | #: állapotváltozásáról $p-V$, $T-V$ és $T-p$ koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!</wlatex><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex> A görbék megszerkesztéséhez $p-V$ diagramban $pV=n R\cdot T$ állapotegyenletből és adiabatita egyenletéből indulunk ki. |
| − | + | * $p-V$ diagramban $p V^\gamma=\mathrm{const.}$, $\gamma = \frac{f+2}{f}> 1$. | |
* $T-V$ diagramban az adiabata egyenletét $\frac{pV}{T}=\mathrm{conts.}$ egyenletel osztva $T V^{\gamma-1}=\mathrm{const.}$ görbét ábrázoljuk. | * $T-V$ diagramban az adiabata egyenletét $\frac{pV}{T}=\mathrm{conts.}$ egyenletel osztva $T V^{\gamma-1}=\mathrm{const.}$ görbét ábrázoljuk. | ||
* $T-p$ diagramban az előző egyenletet $p^{\frac{\gamma-1}{\gamma}} V^{\frac{\gamma-1}{\gamma}\gamma}=\mathrm{const.}$ egyenlettel osztva $T p^{\frac{1-\gamma}{\gamma}}=\mathrm{const.}$ ábrázolandó összefüggést nyerjük. | * $T-p$ diagramban az előző egyenletet $p^{\frac{\gamma-1}{\gamma}} V^{\frac{\gamma-1}{\gamma}\gamma}=\mathrm{const.}$ egyenlettel osztva $T p^{\frac{1-\gamma}{\gamma}}=\mathrm{const.}$ ábrázolandó összefüggést nyerjük. | ||
A lap 2013. április 6., 15:58-kori változata
Feladat
- Készítsen vázlatos ábrát ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásáról
, 
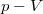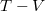és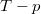 
koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!
Megoldás
A görbék megszerkesztéséhezállapotegyenletből és adiabatita egyenletéből indulunk ki.
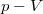- diagramban
, 
.
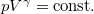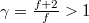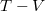- diagramban az adiabata egyenletét
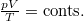egyenletel osztva 
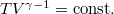görbét ábrázoljuk.
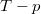- diagramban az előző egyenletet
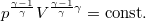egyenlettel osztva 
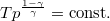ábrázolandó összefüggést nyerjük.
Fontos megfigyelni, melyik görbe milyen meredekséggel érkezik (elméletben) az origóba.
