„Termodinamika példák - Térfogatváltozás fajhőviszonnyal” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 11. sor: | 11. sor: | ||
</noinclude><wlatex># Egy kezdetben $V_1$ térfogatú, $\gamma$ fajhőviszonyú ideális gáz térfogatát $V_2$-re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya $2$. Mekkora a $V_2$ térfogat?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$V_2=V_1\,2\frac{1}{\gamma-1}$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># Egy kezdetben $V_1$ térfogatú, $\gamma$ fajhőviszonyú ideális gáz térfogatát $V_2$-re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya $2$. Mekkora a $V_2$ térfogat?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$V_2=V_1\,2\frac{1}{\gamma-1}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Azonos kezdeti feltételekből izoterm állapotváltozás során |
| + | $$ p_1 V_1 = p_{2\text{T}} V_2 $$ | ||
| + | míg adiabatikusan | ||
| + | $$ p_1 V_1^\gamma = p_{2\text{ad}} V_2^\gamma. $$ | ||
| + | |||
| + | A két egyenletet egymással elosztva | ||
| + | $$ V_1^{\gamma-1} = \frac{p_{2\text{ad}}}{p_{2\text{T}}} V_2^{\gamma-1}, $$ | ||
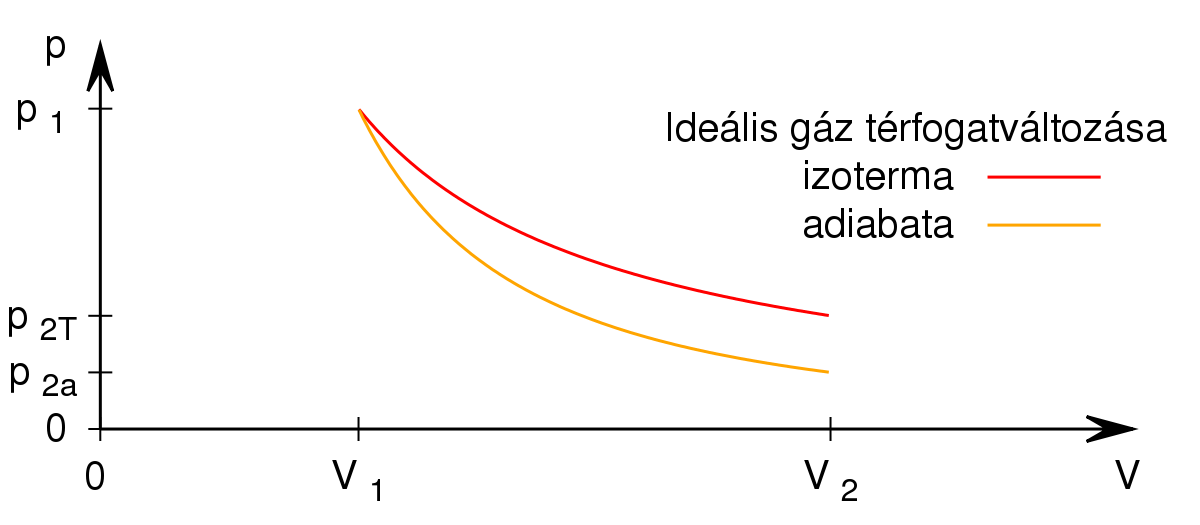
| + | ahol a feladat szerint $\frac{p_{2\text{T}}{p_{2\text{ad}}=2$ (táguláskor az 1:2 arány csak ebben az irányban teljesülhet, mert az adiabata meredekebb, mint az izoterma), innen | ||
| + | $$ V_2 = V_1 \cdot 2^{\frac{1}{\gamma-1}}$$ | ||
| + | |||
| + | [[Fájl:Ideális gáz térfogatváltozása.svg]] | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 7., 14:50-kori változata
Feladat
- Egy kezdetben
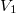térfogatú, 
fajhőviszonyú ideális gáz térfogatát 
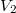-re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya 
. Mekkora a 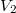térfogat?
Megoldás
Azonos kezdeti feltételekből izoterm állapotváltozás során
![\[ p_1 V_1 = p_{2\text{T}} V_2 \]](/images/math/a/5/a/a5a66c3fbf0a42b787c99a18f6ebbf45.png)
míg adiabatikusan
![\[ p_1 V_1^\gamma = p_{2\text{ad}} V_2^\gamma. \]](/images/math/4/5/8/4586ba149c481541b21d8195f02bd026.png)
A két egyenletet egymással elosztva
![\[ V_1^{\gamma-1} = \frac{p_{2\text{ad}}}{p_{2\text{T}}} V_2^{\gamma-1}, \]](/images/math/4/c/b/4cb48b4ac50bf60bf5820a17352434cf.png)
\setbox0\hbox{$\frac{p_{2\text{T}}{p_{2\text{ad}}=2$}%
\message{//depth:\the\dp0//}%
\box0%
(táguláskor az 1:2 arány csak ebben az irányban teljesülhet, mert az adiabata meredekebb, mint az izoterma), innen
![\[ V_2 = V_1 \cdot 2^{\frac{1}{\gamma-1}}\]](/images/math/4/1/e/41e43b63a6e8a9ed8458982dd7aceeb1.png)
