„Termodinamika példák - Átalakulási hő állandó nyomáson” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
|||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő ($L$) az entalpiaváltozással ($\Delta H$) egyenlő!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk az entalpia definícióját és az első főtételt!}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő ($L$) az entalpiaváltozással ($\Delta H$) egyenlő!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk az entalpia definícióját és az első főtételt!}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
Az első főtétel alapján | Az első főtétel alapján | ||
$$ \mathrm{d}U=\delta Q-p\,\mathrm{d}V, $$ | $$ \mathrm{d}U=\delta Q-p\,\mathrm{d}V, $$ | ||
| − | + | amit összehasonlítunk a $H=U+pV$ definícióból adódó | |
$$ \mathrm{d}U = \mathrm{d}H -p\,\mathrm{d}V - V\,\mathrm{d}p$$ | $$ \mathrm{d}U = \mathrm{d}H -p\,\mathrm{d}V - V\,\mathrm{d}p$$ | ||
| − | + | kifejezéssel. | |
Állandó nyomáson tehát | Állandó nyomáson tehát | ||
| − | $$ \delta Q= \mathrm{d}H, $$ | + | $$ \delta Q = \mathrm{d}H, $$ |
| − | amit | + | amit a fázisátalakulásra kiintegrálva |
$$ L=\Delta H. $$ | $$ L=\Delta H. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 24., 18:58-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő (
) az entalpiaváltozással (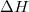
) egyenlő!
Megoldás
Az első főtétel alapján
![\[ \mathrm{d}U=\delta Q-p\,\mathrm{d}V, \]](/images/math/f/e/9/fe9b131e15deeb42877d2d172b821460.png)
amit összehasonlítunk a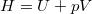 
definícióból adódó
![\[ \mathrm{d}U = \mathrm{d}H -p\,\mathrm{d}V - V\,\mathrm{d}p\]](/images/math/7/1/d/71d81546fe67b6ce8caae31860e9bbd1.png)
kifejezéssel.
Állandó nyomáson tehát
![\[ \delta Q = \mathrm{d}H, \]](/images/math/7/3/7/73716641e99f86e75d0cf100edd3c2ea.png)
amit a fázisátalakulásra kiintegrálva
![\[ L=\Delta H. \]](/images/math/b/0/2/b0292ab2746abf0d1420ebcb978fa64d.png)
