„Termodinamika példák - Diffúzió és belső súrlódás” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
a |
||
| 14. sor: | 14. sor: | ||
#* <wlatex>b) állandó nyomáson?</wlatex><includeonly><wlatex>{{Végeredmény|content=$D$ $n^{3/2}$-szeres, $\eta$ $n^{1/2}$-szeres.}}</wlatex></includeonly><noinclude> | #* <wlatex>b) állandó nyomáson?</wlatex><includeonly><wlatex>{{Végeredmény|content=$D$ $n^{3/2}$-szeres, $\eta$ $n^{1/2}$-szeres.}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A diffúzióállandó értéke (vö. $\langle J \rangle = -D \frac{\mathrm{d}n_V}{\mathrm{d}z}$ az | + | <wlatex>A diffúzióállandó értéke (vö. $\langle J \rangle = -D \frac{\mathrm{d}n_V}{\mathrm{d}z}$ az részecskeáram-sűrűség) |
$$ D = \frac13 \langle l \rangle \langle v \rangle $$ | $$ D = \frac13 \langle l \rangle \langle v \rangle $$ | ||
képlettel az $\langle l \rangle =\frac1{\sqrt{2}\, n_V \sigma}$ átlagos szabad úthosszból és a $\langle v \rangle =\sqrt{\frac{8kT}{\pi\mu}}$ átlagos molekulasebességből határozható meg. | képlettel az $\langle l \rangle =\frac1{\sqrt{2}\, n_V \sigma}$ átlagos szabad úthosszból és a $\langle v \rangle =\sqrt{\frac{8kT}{\pi\mu}}$ átlagos molekulasebességből határozható meg. | ||
A lap 2013. április 27., 10:17-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Hogyan változik az ideális gáz
 diffúziós állandója és
diffúziós állandója és  belső súrlódási együtthatója, ha a gáz térfogata
belső súrlódási együtthatója, ha a gáz térfogata  -szersére nő
-szersére nő
- a) állandó hőmérsékleten,
- b) állandó nyomáson?
Megoldás
A diffúzióállandó értéke (vö. 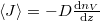 az részecskeáram-sűrűség)
az részecskeáram-sűrűség)
![\[ D = \frac13 \langle l \rangle \langle v \rangle \]](/images/math/b/3/f/b3f1c374e58cec8cabf58f54137a6467.png)
képlettel az 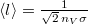 átlagos szabad úthosszból és a
átlagos szabad úthosszból és a 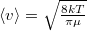 átlagos molekulasebességből határozható meg.
átlagos molekulasebességből határozható meg.
A viszkozitás (vö. 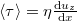 a nyíróerő)
a nyíróerő)
![\[ \eta = -\frac13 \langle l \rangle \langle v \rangle n_V \mu \]](/images/math/c/8/c/c8c9fa0fffa65d1c625b701650e632d3.png)
alakba írható, ahol 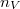 a molekulaszám-sűrűség,
a molekulaszám-sűrűség,  pedig a molekulák tömege.
pedig a molekulák tömege.
Ezek alapján a két mennyiség  és
és  változókkal kifejezve
változókkal kifejezve
![\[ D(T,V) = \frac13 \frac{V}{\sqrt{2}\, N \sigma} \sqrt{\frac{8kT}{\pi\mu}} = \frac{2}{\sigma} \frac{V}{N} \sqrt{\frac{kT}{\pi\mu}} \]](/images/math/7/1/5/71506fee181335b81ffc84a60e684809.png)
![\[ \eta(T,V) = -\frac13 \frac1{\sqrt{2}\, \sigma} \sqrt{\frac{8kT}{\pi\mu}} \,\mu = - \frac2{ 3\sigma} \sqrt{\frac{kT\mu}{\pi}}. \]](/images/math/0/d/a/0da5b2941161ab4b8c2ef700b561510a.png)
a) Állandó hőmérsékleten
![\[ D \propto V, \]](/images/math/3/9/3/3938cf46aeaae956b20825a10d3ee77d.png)
![\[ \eta \propto 1. \]](/images/math/f/6/f/f6fde6bcc6e5cb3e49087c675c836ccd.png)
A diffúziós együttható  -szeresére nől, a viszkozitás állandó marad.
-szeresére nől, a viszkozitás állandó marad.
b) Állandó nyomáson az ideális gáz állapotegyenletéből kifejezzük a hőmérséklet nyomásfüggését:
![\[ pV = NkT \qquad \Rightarrow \qquad \sqrt{T} \propto \sqrt{pV}, \]](/images/math/c/1/b/c1b8ebd7d7bdbd0c60487945c392f3d0.png)
azaz
![\[ D \propto V^{3/2}, \]](/images/math/f/6/b/f6b04dbcf6e9fd06633f3766b77a2f96.png)
![\[ \eta \propto \sqrt V. \]](/images/math/5/4/d/54d92759533429a759900d651fa61d18.png)
A diffúziós együttható 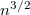 -szeresére, a viszkozitás
-szeresére, a viszkozitás 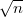 -szeresére nől.
-szeresére nől.