|
|
| 8. sor: |
8. sor: |
| | }} | | }} |
| | == Feladat == | | == Feladat == |
| − | </noinclude><wlatex>#Határozzuk meg egy $I$ áram által átjárt véges hosszúságú egyenes vezető mágneses terét a vezetőtől $d$ távolságra található az $O$ pontban. A vezető szakasz egyik vége $O$ pontból $\alpha_1$, míg a másik vége $\alpha_2$ szög alatt látszódik az $O$-ból a vezetőre állított merőlegeshez képest.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}$$}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex>#Határozzuk meg az áramvonalak törési törvényét a $\sigma_1$ és $\sigma_2$ vezetőképességű közegek határán.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)$$}} |
| | + | </wlatex></includeonly><noinclude> |
| | == Megoldás == | | == Megoldás == |
| | <wlatex> | | <wlatex> |
| − | a.) A mágneses tér meghatározható, ha a Biot-Savart törvényt kiintegráljuk a vezető teljes hossza mentén: | + | Legyen $\alpha_1$ és $\alpha_2$ az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó. |
| | + | $$\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) $$ |
| | | | |
| − | $$B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{dl\times r}{\mid r \mid ^3}$$ | + | Az örvénymentességből pedig következik, hogy az elektromos tér felületre párhuzamos komponense folytonosan megy át: |
| | + | $$E_{1t} = E_{2t} $$ |
| | + | Ebbe a differenciális Ohm-törvényt beírva: |
| | + | $$\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}$$ |
| | | | |
| − | Ahol $dl$ az áramjárta vezető elemi darabja, $r$ pedig az elemi vezetődarabtól a tér vizsgált pontjába mutató vektor. A tér vizsgált pontját nevezzük ki a koordináta-rendszer origójának ($O$). Ettől $d$ távolságra, az $y$ tengellyel párhuzamosan helyezkedik el az áramjárta vezető. Parametrizáljuk a vezető pontjait a vezető adott pontjából az origóba húzott $r$ sugár $x$ tengellyel bezárt $\varphi$ szögével az ábra szerint.
| + | A kapott két egyenletet elosztva, kiesik az áramsűrűség, és azt kapjuk: |
| − | 1.ábra
| + | |
| | | | |
| − | Fejezzünk ki a Biot-Savart integrál változóit $\varphi$ függvényében!
| + | $$\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)$$ |
| − | | + | |
| − | $$r=\dfrac{d}{\cos (\varphi)}$$
| + | |
| − | | + | |
| − | Az $A$ és $A''$ pontok közti infinitezimális $dl$ vezetőszakasz az $O$ pontból $d\varphi$ szög alatt látszik. Az $O$ $A''$ szakaszon kijelölünk egy $A'$ pontot úgy, hogy $OA'=r$. Belátható, hogy az $AA'$ szakasz hossza közelítőleg megegyezik egy $d\varphi$ szög alatt látszó $r$ sugarú ívelemmel:
| + | |
| − | | + | |
| − | $$ AA'=r d\varphi$$
| + | |
| − | | + | |
| − | Mivel $AOP$ és $A''AA'$ merőleges szárú szögek, ezért $A''AA'=\varphi$. Ezek alapján:
| + | |
| − | | + | |
| − | $$dl=\dfrac{AA'}{\cos (\varphi)}=\dfrac{r}{\cos(\varphi)}d\varphi=\dfrac{d}{\cos^2(\varphi)}d\varphi$$
| + | |
| − | | + | |
| − | A Biot-Savart törvényben szereplő vektorszorzat a vezető minden $dl$ eleme esetén az ábra síkjára merőleges, befelé mutató mágneses indukció járulékot ad. Emiatt a vektorszorzatot az alábbiak szerint egyszerűsíthetjük:
| + | |
| − | | + | |
| − | $$B=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid \mid r \mid sin(A''AP)}{\mid r \mid ^3}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\mid dl\ \mid sin(A''AP)}{\mid r \mid ^2}=$$
| + | |
| − | | + | |
| − | $$=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ \left( \dfrac{d}{\cos^2(\varphi)} \right) sin(A''AP)}{ \left( \dfrac{d}{\cos(\varphi)} \right)^2 }d\varphi=\dfrac{\mu_0 I}{4 \pi} \int_{\alpha_1}^{\alpha_2} \dfrac{ sin(A''AP)}{ d }d\varphi$$
| + | |
| − | | + | |
| − | Az ábra alapján a szinusz argumentumában szereplő $A''AP$ szögről beláthatjuk, hogy:
| + | |
| − | | + | |
| − | $$A''AP=180-OAP=180-(90-\varphi)=90+\varphi$$
| + | |
| − | | + | |
| − | Tehát:
| + | |
| − | | + | |
| − | $$\sin(A''AP)=\cos(\varphi)$$
| + | |
| − | | + | |
| − | A Biot-Savart integrál tehát tovább egyszerűsödik:
| + | |
| − | | + | |
| − | $$B=\dfrac{\mu_0 I}{4 \pi d} \int_{\alpha_1}^{\alpha_2} cos(\varphi) d\varphi =\dfrac{\mu_0 I}{4 \pi d}\left( \sin(\alpha_1)-sin(\alpha_2) \right) $$
| + | |
| − | | + | |
| − | A véges hosszúságú áramjárta vezető mágneses terének nagysága tehát:
| + | |
| − | | + | |
| − | $$B=\dfrac{\mu_0 I}{4 \pi d}\left( \sin(\alpha_1)-sin(\alpha_2) \right) $$
| + | |
| − | | + | |
| − | Iránya pedig az ábra síkjára merőlegesen kifelé mutat.
| + | |
| − | | + | |
| − | Megjegyzés
| + | |
| − | | + | |
| − | Az eredményt érdemes megjegyezni, hiszen a későbbiekben gyakran találkozunk olyan áramjárta vezető geometriákkal, melyek véges egyenes szakaszokból tevődnek össze. Külön figyelmet érdemel a végtelen vezetőre vonatkozó határeset, amikor $\alpha_1=\pi /2$ és $\alpha_2=-\pi /2$. Ilyenkor a tér:
| + | |
| − | | + | |
| − | $$B=\dfrac{\mu_0 I}{4 \pi d} (1-(-1))=\dfrac{\mu_0 I}{2 \pi d}$$
| + | |
| − | | + | |
| − | Az eredmény megnyugtató összhangban van a végtelen egyenes vezető Amper-féle gerjesztési törvénnyel kiszámolt terével: [[Magnetosztatika példák - Egyenes vezető mágneses tere 2|Egyenes vezető mágneses tere 2]]
| + | |
| | </wlatex> | | </wlatex> |
| | </noinclude> | | </noinclude> |
Az örvénymentességből pedig következik, hogy az elektromos tér felületre párhuzamos komponense folytonosan megy át:
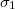és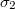 
vezetőképességű közegek határán.
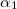és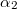 
az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
![\[\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) \]](/images/math/8/2/7/827afd735af94c884dc0fc233fb2b9ca.png)
![\[E_{1t} = E_{2t} \]](/images/math/d/5/9/d59760c33230de53eb5d60da46323704.png)
![\[\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}\]](/images/math/0/2/9/029ee907ef9cee8ec9ebb36074712905.png)
![\[\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)\]](/images/math/a/9/b/a9b91a5d5a4e80746e75088230a80969.png)
