„Termodinamika példák - Nyomás hőmérsékletfüggése mérhető mennyiségekkel” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># A $p=p(T,V)$ állapotegyenlet ismeretében fejezzük ki a $\left(\frac{\partial p}{\partial T}\right)_V$ mennyiséget a | + | </noinclude><wlatex># A $p=p(T,V)$ állapotegyenlet ismeretében fejezzük ki a $\left(\frac{\partial p}{\partial T}\right)_V$ mennyiséget a $\beta_p$ hőtágulási együttható és a $\kappa_T$ izotermikus kompresszibilitás segítségével!</wlatex><includeonly><wlatex>{{Útmutatás|content=Használja fel a két mennyiség definícióját és azt, hogy állandó nyomáson a $\rm{d}\,p$ teljes differenciál nulla.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>Megoldás szövege. | <wlatex>Megoldás szövege. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2012. november 17., 22:27-kori változata
Feladat
- A
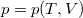állapotegyenlet ismeretében fejezzük ki a 
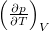mennyiséget a 
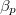hőtágulási együttható és a 
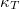izotermikus kompresszibilitás segítségével!
Megoldás
Megoldás szövege.
