„Termodinamika példák - Vákuum” változatai közötti eltérés
A Fizipedia wikiből
| 16. sor: | 16. sor: | ||
</noinclude><wlatex># Legfeljebb mekkora lehet az $1\,\mathrm{l}$ térfogatú, gömb alakú edényben lévő $300\,\mathrm{K}$-es hidrogéngáz nyomása, hogy az átlagos szabad úthossz nagyobb legyen az edény átmérőjénél? A hidrogénmolekula átmérője $2\cdot10^{-10}\,\mathrm{m}$.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$p<0,155\,\mathrm{Pa}$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># Legfeljebb mekkora lehet az $1\,\mathrm{l}$ térfogatú, gömb alakú edényben lévő $300\,\mathrm{K}$-es hidrogéngáz nyomása, hogy az átlagos szabad úthossz nagyobb legyen az edény átmérőjénél? A hidrogénmolekula átmérője $2\cdot10^{-10}\,\mathrm{m}$.</wlatex><includeonly><wlatex>{{Végeredmény|content=$$p<0,155\,\mathrm{Pa}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex> |
| + | Az átlagos szabad úthossz | ||
| + | $$\bar l=\frac1{\sqrt 2 n_V \sigma},$$ | ||
| + | ahol $\sigma$ a részecskék ütközési hatáskeresztmetszete, $n_V$ pedig a gáz molekulaszám-sűrűsége. Klasszikus kinetikus modellben a szórási hatáskeresztmetszetet a molekulák, mint „kemény gömbök” vetületi területével adjuk meg, amit a $d$ átmérővel fejezhetünk ki: | ||
| + | $$ \sigma = d^2 \pi. $$ | ||
| + | Az ideális gáz $pV=NkT$ állapotegyenletéből meghatározhatjuk a molekulaszám-sűrűséget: | ||
| + | $$ n_V = \frac{N}{V}=\frac{p}{kT}.$$ | ||
| + | |||
| + | A $ 2R < \bar l$ megkövetelt feltétel behelyettesítve: | ||
| + | $$ 2R < \frac{kT}{\sqrt 2 p d^2\pi}, $$ | ||
| + | ebből átrendezéssel a nyomás: | ||
| + | $$ p < \frac{kT}{2\sqrt 2 R d^2\pi}. $$ | ||
| + | |||
| + | A számszerű adatok pedig: $R=\displaystyle\left(\frac{3 \cdot 1\,\mathrm{dm}^3}{4\pi}\right)^{1/3}\approx 0,062\,\mathrm{m}$, $k=1,39 \cdot 10^{-23}\,\mathrm{J}/\mathrm{K}$, $T=300\,\mathrm{K}$ és $d=10^{-10}\,\mathrm{m}$, amivel $p<0,155\,\mathrm{Pa}$. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. március 23., 20:27-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Legfeljebb mekkora lehet az
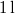térfogatú, gömb alakú edényben lévő 
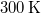-es hidrogéngáz nyomása, hogy az átlagos szabad úthossz nagyobb legyen az edény átmérőjénél? A hidrogénmolekula átmérője 
.
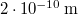Megoldás
Az átlagos szabad úthossz
![\[\bar l=\frac1{\sqrt 2 n_V \sigma},\]](/images/math/7/c/d/7cd94c117fd2f118c19668a5857f19fa.png)
ahol 
a részecskék ütközési hatáskeresztmetszete, 
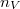pedig a gáz molekulaszám-sűrűsége. Klasszikus kinetikus modellben a szórási hatáskeresztmetszetet a molekulák, mint „kemény gömbök” vetületi területével adjuk meg, amit a 
átmérővel fejezhetünk ki:
![\[ \sigma = d^2 \pi. \]](/images/math/c/2/2/c224eeccfeb0354f9a5e3b7f5000a234.png)
Az ideális gáz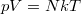 
állapotegyenletéből meghatározhatjuk a molekulaszám-sűrűséget:
![\[ n_V = \frac{N}{V}=\frac{p}{kT}.\]](/images/math/a/0/4/a04cf2a3daa52158e8c2c986fe939bad.png)
A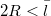 
megkövetelt feltétel behelyettesítve:
![\[ 2R < \frac{kT}{\sqrt 2 p d^2\pi}, \]](/images/math/1/1/5/115b83404c18af7421f96883ef5ded4a.png)
ebből átrendezéssel a nyomás:
![\[ p < \frac{kT}{2\sqrt 2 R d^2\pi}. \]](/images/math/4/8/7/487811d3b6102a084cfcb41df4504df3.png)
A számszerű adatok pedig: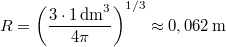 
, 
, 
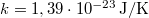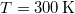és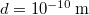 
, amivel 
.
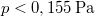