„Termodinamika példák - Diffúzió és belső súrlódás” változatai közötti eltérés

A Fizipedia wikiből
18. sor: 18. sor:
 
#* <wlatex>b) állandó nyomáson?</wlatex><includeonly><wlatex>{{Végeredmény|content=$D$ $n^{3/2}$-szeres, $\eta$ $n^{1/2}$-szeres.}}</wlatex></includeonly><noinclude>
 
#* <wlatex>b) állandó nyomáson?</wlatex><includeonly><wlatex>{{Végeredmény|content=$D$ $n^{3/2}$-szeres, $\eta$ $n^{1/2}$-szeres.}}</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>
 +
A diffúzióállandó (vö. $\bar J = -D \frac{\mathrm{d}n_V}{\mathrm{d}z}$ az részecske-áramsűrűség)
 +
$$ D = \frac13\bar l\bar v $$
 +
képlettel az $\bar l=\frac1{\sqrt 2 n_V \sigma}$ átlagos szabad úthosszból és a $\bar v=\sqrt{\frac{8kT}{\pi\mu}}$ átlagos molekulasebességből határozható meg.
 +
 
 +
A viszkozitás (vö. $\bar \tau = \eta \frac{\mathrm{d}u_z}{\mathrm{d}x}$ a nyíróerő)
 +
$$ \eta = -\frac13 \bar l \bar v n_V \mu $$
 +
alakba írható, ahol $n_V$ a molekulaszám-sűrűség, $\mu$ pedig a molekulák tömege.
 +
 
 +
Behelyettesítve
 +
$$ D(T,V) = \frac13 \frac{V}{\sqrt 2 N \sigma} \sqrt{\frac{8kT}{\pi\mu}}
 +
= \frac2{\sigma} \frac{V}{N} \sqrt{\frac{kT}{\pi\mu}} $$
 +
 
 +
$$ \eta(T,V)= -\frac13 \frac1{\sqrt 2 \sigma} \sqrt{\frac{8kT}{\pi\mu}} \mu =
 +
- \frac2{ 3\sigma} \sqrt{\frac{kT\mu}{\pi}} $$
 +
 
 +
 
 +
* (a) állandó hőmérsékleten
 +
$$ D \propto V $$
 +
$$ \eta \propto 1 $$
 +
A diffúziós együttható $n$-szeresére nől, a viszkozitás állandó marad.
 +
* (b) állandó nyomáson az egyetemes gáztörvényből kifejezzük a hőmérséklet nyomásfüggését:
 +
$$ pV = NkT \qquad \Rightarrow \qquad \sqrt{T} \propto \sqrt{pV}, $$
 +
azaz
 +
$$ D \propto V^{3/2}$$
 +
$$ \eta \propto \sqrt V $$
 +
A diffúziós együttható $n^{3/2}$-szeresére, a viszkozitás $\sqrt{n}$-szeresére nől.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. március 23., 21:14-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Termodinamika - Kinetikus gázelmélet, transzportfolyamatok
Feladatok listája:
  1. Id. g. nyomása belső energiával
  2. Stern-kísérlet
  3. Energia szerinti eloszlás
  4. Vákuum
  5. Diffúzió és belső súrlódás
  6. Gáz szökése
  7. Gázcsere tartályok közt
  8. Gázcsere két gázzal
  9. Lineáris hőmérsékletprofil
  10. Jég fagyása
  11. Hővezetés
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Hogyan változik az ideális gáz \setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0% diffúziós állandója és \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% belső súrlódási együtthatója, ha a gáz térfogata \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%-szersére nő
    • a) állandó hőmérsékleten,
    • b) állandó nyomáson?

Megoldás


A diffúzióállandó (vö. \setbox0\hbox{$\bar J = -D \frac{\mathrm{d}n_V}{\mathrm{d}z}$}% \message{//depth:\the\dp0//}% \box0% az részecske-áramsűrűség)

\[ D = \frac13\bar l\bar v \]

képlettel az 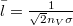\setbox0\hbox{$\bar l=\frac1{\sqrt 2 n_V \sigma}$}% \message{//depth:\the\dp0//}% \box0% átlagos szabad úthosszból és a 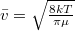\setbox0\hbox{$\bar v=\sqrt{\frac{8kT}{\pi\mu}}$}% \message{//depth:\the\dp0//}% \box0% átlagos molekulasebességből határozható meg.

A viszkozitás (vö. 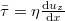\setbox0\hbox{$\bar \tau = \eta \frac{\mathrm{d}u_z}{\mathrm{d}x}$}% \message{//depth:\the\dp0//}% \box0% a nyíróerő)

\[ \eta = -\frac13 \bar l \bar v n_V \mu \]

alakba írható, ahol 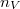\setbox0\hbox{$n_V$}% \message{//depth:\the\dp0//}% \box0% a molekulaszám-sűrűség, \setbox0\hbox{$\mu$}% \message{//depth:\the\dp0//}% \box0% pedig a molekulák tömege.

Behelyettesítve

\[ D(T,V) = \frac13 \frac{V}{\sqrt 2 N \sigma} \sqrt{\frac{8kT}{\pi\mu}} = \frac2{\sigma} \frac{V}{N} \sqrt{\frac{kT}{\pi\mu}} \]
\[ \eta(T,V)= -\frac13 \frac1{\sqrt 2 \sigma} \sqrt{\frac{8kT}{\pi\mu}} \mu = - \frac2{ 3\sigma} \sqrt{\frac{kT\mu}{\pi}} \]


  • (a) állandó hőmérsékleten
\[ D \propto V \]
\[ \eta \propto 1 \]

A diffúziós együttható \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%-szeresére nől, a viszkozitás állandó marad.

  • (b) állandó nyomáson az egyetemes gáztörvényből kifejezzük a hőmérséklet nyomásfüggését:
\[ pV = NkT \qquad \Rightarrow \qquad \sqrt{T} \propto \sqrt{pV}, \]

azaz

\[ D \propto V^{3/2}\]
\[ \eta \propto \sqrt V \]

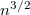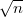A diffúziós együttható \setbox0\hbox{$n^{3/2}$}% \message{//depth:\the\dp0//}% \box0%-szeresére, a viszkozitás \setbox0\hbox{$\sqrt{n}$}% \message{//depth:\the\dp0//}% \box0%-szeresére nől.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Diffúzió_és_belső_súrlódás&oldid=8053”