„Termodinamika példák - Energia-összefüggések fajhőviszonnyal” változatai közötti eltérés
A Fizipedia wikiből
| 25. sor: | 25. sor: | ||
Ezzel | Ezzel | ||
| − | $$\Delta U | + | $$\Delta U = \frac{\Delta W}{\gamma-1}$$ |
Az egyetemes gázállandó és a fajhők közötti kapcsolatot egyik fajhő definíciójából vezethetjük le: | Az egyetemes gázállandó és a fajhők közötti kapcsolatot egyik fajhő definíciójából vezethetjük le: | ||
| 33. sor: | 33. sor: | ||
$$ C_p = \left(\frac f 2+1\right)R = C_V+R = \frac{\gamma}{\gamma-1}R, $$ | $$ C_p = \left(\frac f 2+1\right)R = C_V+R = \frac{\gamma}{\gamma-1}R, $$ | ||
amiből | amiből | ||
| − | $$ \Delta Q = \frac{\gamma }{\gamma -1}\Delta W = \gamma\Delta U.$$ | + | $$ \Delta Q = \frac{\gamma}{\gamma-1}\Delta W = \gamma\Delta U.$$ |
| + | |||
| + | == Megjegyzés == | ||
| + | Egy másik lehetőség az egyetemes gázállandó és a fajhők közötti kapcsolat megteremtésére, hogy állandó térfogaton | ||
| + | $$ \Delta U = \delta Q = n C_V \Delta T, $$ | ||
| + | amit $\Delta U = \frac{f}{2}nR\Delta T$-val összevetve szintén | ||
| + | $$ C_V = \frac{f}{2}R. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 6., 18:38-kori változata
Feladat
- Állapítsuk meg, milyen összefüggés van egy ideális gáz által állandó nyomáson végzett
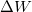 munka, a gázzal közölt
munka, a gázzal közölt 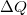 hőmennyiség és a
hőmennyiség és a 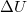 belső energia-változás között, ha a
belső energia-változás között, ha a  fajhőviszony ismert!
fajhőviszony ismert!
Megoldás
Mivel a nyomás állandó, a gáz által végzett munka szorzatalakban felírható, amit az első főtétel segítségével tovább alakítunk:
![\[ \Delta W = p\Delta V = nR\Delta T.\]](/images/math/5/b/2/5b2567d9a6aaf2dcc21af70b92ce5013.png)
Az ekvipartíció tétele értelmében az ideális gáz belső energiája kifejezhető a hőmérsékletével, így a belső energia megváltozása is:
![\[ \Delta U = \frac{f}{2}nR\Delta T = \frac f 2\Delta W.\]](/images/math/1/6/5/165cd1508142e42931eeabf8f107aaf5.png)
Az állandó nyomáson a gázzal közölt hő definíció szerint felírható az állandó nyomáson mért fajhővel:
![\[ \Delta Q = C_pn\Delta T = \frac{C_p}{R} \Delta W.\]](/images/math/8/4/2/842da83c25344e4751aec1ec8f8d9a70.png)
A  fajhőviszony és a gáz
fajhőviszony és a gáz  szabadsági fokai közti összefüggést alakítjuk:
szabadsági fokai közti összefüggést alakítjuk:
![\[ \gamma = \frac{C_p}{C_V} = \frac{f+2}{f},\]](/images/math/8/2/2/822832f3865873a7eddc0a2b477e611d.png)
![\[ \frac{f}{2} = \frac{1}{\gamma-1}.\]](/images/math/8/3/4/834d315b61a5fa043fe72585f496afed.png)
Ezzel
![\[\Delta U = \frac{\Delta W}{\gamma-1}\]](/images/math/e/f/3/ef388cea80a3b527aa19f573a0186d20.png)
Az egyetemes gázállandó és a fajhők közötti kapcsolatot egyik fajhő definíciójából vezethetjük le:
![\[ C_V = \frac{1}{n}\frac{\mathrm{d}U}{\mathrm{d}T} = \frac{f}{2}R. \]](/images/math/6/8/3/683d597a5468b347cf48074ed1001309.png)
A fajhőviszony segítségével
![\[ C_p = \left(\frac f 2+1\right)R = C_V+R = \frac{\gamma}{\gamma-1}R, \]](/images/math/7/7/3/773f25f617e7f2d54af0570d8dc4cb9e.png)
amiből
![\[ \Delta Q = \frac{\gamma}{\gamma-1}\Delta W = \gamma\Delta U.\]](/images/math/2/8/6/2865d7fb0d87f46fe411fa468f76cacf.png)
Megjegyzés
Egy másik lehetőség az egyetemes gázállandó és a fajhők közötti kapcsolat megteremtésére, hogy állandó térfogaton
![\[ \Delta U = \delta Q = n C_V \Delta T, \]](/images/math/3/c/3/3c37e70a9704d7764e0c14b8dcd12c7b.png)
amit 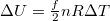 -val összevetve szintén
-val összevetve szintén
![\[ C_V = \frac{f}{2}R. \]](/images/math/1/7/f/17f647005bd33283a7f2e8d5c1b7dfba.png)