„Termodinamika példák - Nyomás hőmérsékletfüggése mérhető mennyiségekkel” változatai közötti eltérés
A Fizipedia wikiből
a (→Megoldás) |
|||
| 23. sor: | 23. sor: | ||
= \frac{\beta_p}{\kappa_ T}$$ | = \frac{\beta_p}{\kappa_ T}$$ | ||
| − | * | + | * Gyorsabban juthatunk el az eredményhez izochor folyamattal: |
$$ \mathrm{d}V = 0 = {\left(\frac{\partial V}{\partial T}\right)}_p \mathrm{d}T + {\left(\frac{\partial V}{\partial p}\right)}_T \mathrm{d}p | $$ \mathrm{d}V = 0 = {\left(\frac{\partial V}{\partial T}\right)}_p \mathrm{d}T + {\left(\frac{\partial V}{\partial p}\right)}_T \mathrm{d}p | ||
| − | = V\beta_p \mathrm{d}T - V\kappa_T \mathrm{d}p $$ | + | = V\beta_p \,\mathrm{d}T - V\kappa_T \,\mathrm{d}p $$ |
formálisan osztunk $\mathrm{d}T$-vel és jelöljük kell az izochor állapotváltozást: | formálisan osztunk $\mathrm{d}T$-vel és jelöljük kell az izochor állapotváltozást: | ||
$$ {\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}. $$ | $$ {\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 7., 00:01-kori változata
Feladat
- A
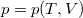állapotegyenlet ismeretében fejezzük ki a 
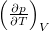mennyiséget a 
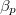hőtágulási együttható és a 
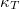izotermikus kompresszibilitás segítségével!
Megoldás
Az izobár hőtágulási együttható és az izoterm kompresszibilitás rendre
![\[{\beta }_ p\mathrm{\colon }=\frac 1 V{\left(\frac{\partial V}{\partial T}\right)}_ p, \qquad {\kappa }_ T\mathrm{\colon }=-\frac 1 V{\left(\frac{\partial V}{\partial p}\right)}_ T\]](/images/math/0/f/1/0f1f416348967fbb697a62cc6ac1c4df.png)
- Izobár folyamatban
![\[ \mathrm{d}p = 0 = {\left(\frac{\partial p}{\partial T}\right)}_V \mathrm{d}T + {\left(\frac{\partial p}{\partial V}\right)}_T \mathrm{d}V, \]](/images/math/8/c/2/8c2cdf644a292873b9d25df24dd57aa5.png)
és a formális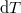 
-vel osztás során jelölnünk kell az izobár állapotváltozást:
![\[ {\left(\frac{\partial p}{\partial T}\right)}_V = -{\left(\frac{\partial p}{\partial V}\right)}_T {\left(\frac{\partial V}{\partial T}\right)}_p = \frac 1{V\kappa_T}\cdot V\beta_p = \frac{\beta_p}{\kappa_ T}\]](/images/math/9/e/b/9eb277917c413c57e4824c5c3b3d5a95.png)
- Gyorsabban juthatunk el az eredményhez izochor folyamattal:
![\[ \mathrm{d}V = 0 = {\left(\frac{\partial V}{\partial T}\right)}_p \mathrm{d}T + {\left(\frac{\partial V}{\partial p}\right)}_T \mathrm{d}p = V\beta_p \,\mathrm{d}T - V\kappa_T \,\mathrm{d}p \]](/images/math/f/1/a/f1af5c47b6c9f91eee622a02be29e23f.png)
formálisan osztunk 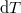-vel és jelöljük kell az izochor állapotváltozást:
![\[ {\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}. \]](/images/math/c/4/f/c4fcbf429061d44dfada22dc0e50cdfe.png)
