„Termodinamika példák - Ideális gáz entrópiája” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Termodinamika - Entrópia, II. főtétel {{Kísérleti fizi…”) |
|||
| 14. sor: | 14. sor: | ||
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$S_0=-nR\ln n+ns_0,$$ amivel az entrópia $$S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,$$ ahol $s_0$ már $n$-től független.}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$S_0=-nR\ln n+ns_0,$$ amivel az entrópia $$S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,$$ ahol $s_0$ már $n$-től független.}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>'''a)''' Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája a részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az $S_0$ referenciaérték függ a rendszer nagyságától, azaz a mólszámtól. |
| + | |||
| + | '''b)''' A feladatban megadott képletben $\ln T$ és $\ln V$ csak dimenzió nélkül (előre rögzített $T_0$ és $V_0$ egységekben mért mértékegység nélküli számként) értelmezhetőek, ahogy az [[Termodinamika példák - Az entrópia hőmérséklet és térfogatfüggése, az adiabata egyenlete|előző feladatban]] megállapítottuk: | ||
| + | $$ S\left(T,V\right)- S_0=n\left( C_V \ln T + R\ln V \right)$$ | ||
| + | |||
| + | Láthatóan a kifejezést $n$-nel osztva a kapott $S_M$ moláris entrópia változása már nem függ a mólszámtól, így $S_M$ és $S_M^0$ sem. | ||
| + | $$ S_0\left(n\right)=n\cdot S_M^0 $$ | ||
| + | |||
| + | Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést: | ||
| + | $$ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right).$$ | ||
| + | Az $s_0=R\ln n + S_M^0$ definícióval $s_0$ már első rendben független a mólszámtól, és beazonosíthatjuk, hogy $S_0=-nR\ln n+ns_0$. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 13., 23:43-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az ideális gáz entrópiáját gyakran az
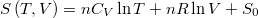alakban használják.
- a) Indokolja meg, hogy az
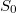mennyiségnek függnie kell a rendszer anyagmennyiségét megadó n mólszámtól!
- b) Adjon meg egy olyan
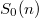·függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!
- a) Indokolja meg, hogy az
Megoldás
a) Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája a részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az 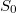referenciaérték függ a rendszer nagyságától, azaz a mólszámtól.
b) A feladatban megadott képletben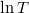 
és 
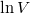csak dimenzió nélkül (előre rögzített 
és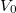 
egységekben mért mértékegység nélküli számként) értelmezhetőek, ahogy az előző feladatban megállapítottuk:
![\[ S\left(T,V\right)- S_0=n\left( C_V \ln T + R\ln V \right)\]](/images/math/6/3/8/6387b3aa6da8ef4bb5c7d6bd4e0db5b1.png)
Láthatóan a kifejezést 
-nel osztva a kapott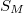 
moláris entrópia változása már nem függ a mólszámtól, így 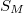és 
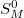sem.
![\[ S_0\left(n\right)=n\cdot S_M^0 \]](/images/math/c/e/d/cedabda1504ae89eced9b3550e1f1861.png)
Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést:
![\[ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right).\]](/images/math/2/1/0/2102b82bfe78372c8771561ef163cb59.png)
Az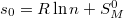 
definícióval 
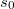már első rendben független a mólszámtól, és beazonosíthatjuk, hogy 
.
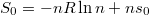