„Termodinamika példák - Ideális gáz entrópiája” változatai közötti eltérés
A Fizipedia wikiből
| 11. sor: | 11. sor: | ||
</noinclude><wlatex># Az ideális gáz entrópiáját gyakran az $S\left(T,V\right)=n C_V\ln T+nR\ln V+ S_0$ alakban használják.</wlatex> | </noinclude><wlatex># Az ideális gáz entrópiáját gyakran az $S\left(T,V\right)=n C_V\ln T+nR\ln V+ S_0$ alakban használják.</wlatex> | ||
#* a) <wlatex>Indokolja meg, hogy az $S_0$ mennyiségnek függnie kell a rendszer anyagmennyiségét megadó n mólszámtól!</wlatex><includeonly><wlatex>{{Végeredmény|content=Az entrópia extenzív állapotjelző.}}</wlatex></includeonly> | #* a) <wlatex>Indokolja meg, hogy az $S_0$ mennyiségnek függnie kell a rendszer anyagmennyiségét megadó n mólszámtól!</wlatex><includeonly><wlatex>{{Végeredmény|content=Az entrópia extenzív állapotjelző.}}</wlatex></includeonly> | ||
| − | #* b) <wlatex>Adjon meg egy olyan $S_0(n)$ | + | #* b) <wlatex>Adjon meg egy olyan $S_0(n)$-függést, amellyel az entrópia fenti kifejezése teljesíti az ''a)'' pontban szereplő követelményt! |
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$S_0=-nR\ln n+ns_0,$$ amivel az entrópia $$S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,$$ ahol $s_0$ már $n$-től független.}}</wlatex></includeonly><noinclude> | + | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$S_0(n)=-nR\ln n+ns_0,$$ amivel az entrópia $$S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,$$ ahol $s_0$ már $n$-től független.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>'''a)''' Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája a részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az $S_0$ referenciaérték függ a rendszer nagyságától, azaz a mólszámtól. | <wlatex>'''a)''' Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája a részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az $S_0$ referenciaérték függ a rendszer nagyságától, azaz a mólszámtól. | ||
| − | + | ==== Megjegyzés ==== | |
| − | $$ S\left(T,V\right)- S_0=n\left( C_V \ln T + R\ln V \right)$$ | + | A feladatban megadott képletben $\ln T$ és $\ln V$ csak dimenzió nélkül (előre rögzített $T_0$ és $V_0$ egységekben mért mértékegység nélküli számként) értelmezhetőek, ahogy az [[Termodinamika példák - Az entrópia hőmérséklet és térfogatfüggése, az adiabata egyenlete|előző feladatban]] megállapítottuk: |
| + | $$ S\left(T,V,n\right)- S_0(n)=n\left( C_V \ln T + R\ln V \right)$$ | ||
| − | + | '''b)''' Mivel az entrópia extenzív mennyiség, egyensúlyban felírható egy extenzív mennyiség (pl. mólszám) és intenzív mennyiségek összegének szorzataként. Intenzívnek tekintendőek a moláris- és sűrűségjellegű mennyiségek is. | |
| − | + | ||
Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést: | Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést: | ||
| − | $$ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right) | + | $$ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right) |
| − | + | = n\left( C_V \ln T + R\ln V_M + s_0 \right), $$ | |
| + | ahol a zárójelben már intenzív mennyiségek állnak: $ V_M = \frac{V}{n} $ moláris térfogat és $ s_0 = R\ln n + \frac{S_0(n)}{n} $ már független a mólszámtól, és beazonosíthatjuk, hogy | ||
| + | $$ S_0(n)=-nR\ln n+ns_0. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 16., 11:05-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az ideális gáz entrópiáját gyakran az
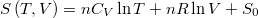alakban használják.
- a) Indokolja meg, hogy az
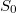mennyiségnek függnie kell a rendszer anyagmennyiségét megadó n mólszámtól!
- b) Adjon meg egy olyan
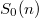-függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!
- a) Indokolja meg, hogy az
Megoldás
a) Az entrópia extenzív mennyiség, ezért egy nagyobb rendszer entrópiája a részrendszerek entrópiájának összege. Ez az additivitás csak úgy teljesülhet, ha az 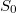referenciaérték függ a rendszer nagyságától, azaz a mólszámtól.
Megjegyzés
A feladatban megadott képletben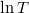 
és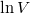 
csak dimenzió nélkül (előre rögzített 
és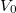 
egységekben mért mértékegység nélküli számként) értelmezhetőek, ahogy az előző feladatban megállapítottuk:
![\[ S\left(T,V,n\right)- S_0(n)=n\left( C_V \ln T + R\ln V \right)\]](/images/math/b/9/5/b9553d68d845abb7505115aa06356f25.png)
b) Mivel az entrópia extenzív mennyiség, egyensúlyban felírható egy extenzív mennyiség (pl. mólszám) és intenzív mennyiségek összegének szorzataként. Intenzívnek tekintendőek a moláris- és sűrűségjellegű mennyiségek is.
Tegyük a térfogatot is molárissá, így leválaszthatjuk a mólszámtól való függést:
![\[ S\left(T,V,n\right) = n\left( C_V \ln T + R\ln \frac{V}{n} + R\ln n +\frac{S_0(n)}{n} \right) = n\left( C_V \ln T + R\ln V_M + s_0 \right), \]](/images/math/e/4/b/e4b84fa24b405361acf517f93bfdba05.png)
ahol a zárójelben már intenzív mennyiségek állnak: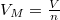 
moláris térfogat és 
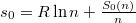már független a mólszámtól, és beazonosíthatjuk, hogy
![\[ S_0(n)=-nR\ln n+ns_0. \]](/images/math/b/1/d/b1dc646b453328d8e2956b16892eeb32.png)
