„Termodinamika példák - Olvadáspont eltolódása nyomásváltozásra” változatai közötti eltérés
A Fizipedia wikiből
| 11. sor: | 11. sor: | ||
</noinclude><wlatex># Felhasználva, hogy az olvadáspont az állandó nyomáson felvett $\mu_p-T$ diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?</wlatex><includeonly><wlatex>{{Útmutatás|content=A nyomásváltozás a $\mu_p-T$ görbét eltolja, mégpedig a két fázisban általában különbözőképpen. A görbe eltolódásának mértékét adott hőmérsékleten, adott fázisban a $$\left(\frac{\partial \mu }{\partial p}\right)_T= V_M$$ összefüggés adja meg.}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># Felhasználva, hogy az olvadáspont az állandó nyomáson felvett $\mu_p-T$ diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?</wlatex><includeonly><wlatex>{{Útmutatás|content=A nyomásváltozás a $\mu_p-T$ görbét eltolja, mégpedig a két fázisban általában különbözőképpen. A görbe eltolódásának mértékét adott hőmérsékleten, adott fázisban a $$\left(\frac{\partial \mu }{\partial p}\right)_T= V_M$$ összefüggés adja meg.}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A [[Termodinamika példák - A termodinamika differenciális összefüggései|differenciális összefüggésekről]] szóló feladatban tárgyaltuk a |
| + | $ G=\mu n$ szabadentalpiára vonatkozó | ||
| + | $$ \left(\frac{\partial G}{\partial p}\right)_T = V $$ | ||
| + | összefüggést, amit most a moláris entrópia és kémiai potenciál kifejezésére használunk: | ||
| + | $$ \left(\frac{\partial \mu }{\partial p}\right)_T=\frac V n = V_M.$$ | ||
| + | |||
| + | ''Az anyagok többségének'' a moláris térfogata szilárd fázisban kisebb, mint folyadék fázisban: | ||
| + | $$ V_M^\text{sz} < V_M^\text{foly},$$ | ||
| + | azaz | ||
| + | $$ \left(\frac{\partial \mu }{\partial p}\right)_T^\text{sz}< \left(\frac{\partial \mu }{\partial p}\right)_T^\text{foly}. $$ | ||
| + | |||
| + | Ez azt jelenti, hogy az [[Termodinamika példák - Kémiai potenciál hőmérsékletfüggése|előző feladatban]] felvázolt $\mu_p(T)$ görbéből úgy kapjuk a nagyobb nyomáshoz tartozó görbét, ha minden egyes $T$ értékhez rendelt $\mu_p$ pontot megnövelünk egy állandó $V_M^* \Delta p>0$ értékkel, de növelés mértéke a folyadék fázisban nagyobb, mint a szilárdban. | ||
| + | |||
| + | Látszik, hogy a két egyenes új metszéspontja $ T_o(p+\Delta p) > T_o (p)$. | ||
| + | |||
| + | ''Víznél'' fagyáskor jelentős térfogatnövekedés lép fel, $V_M^\text{foly} < V_M^\text{sz}$, ugyanezen szerkesztési menetet követve látható, hogy $T_o(p+\Delta p) < T_o (p)$, azaz az új olvadáspont kisebb lesz. | ||
| + | |||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 20., 14:43-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Felhasználva, hogy az olvadáspont az állandó nyomáson felvett
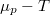 diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
Megoldás
A differenciális összefüggésekről szóló feladatban tárgyaltuk a
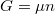 szabadentalpiára vonatkozó
szabadentalpiára vonatkozó
![\[ \left(\frac{\partial G}{\partial p}\right)_T = V \]](/images/math/8/9/f/89f2acfca3b04eb95608e4c9f6746b6f.png)
összefüggést, amit most a moláris entrópia és kémiai potenciál kifejezésére használunk:
![\[ \left(\frac{\partial \mu }{\partial p}\right)_T=\frac V n = V_M.\]](/images/math/1/b/c/1bce37c639e0131c3d9d1abecef914ec.png)
Az anyagok többségének a moláris térfogata szilárd fázisban kisebb, mint folyadék fázisban:
![\[ V_M^\text{sz} < V_M^\text{foly},\]](/images/math/8/d/5/8d51b93a40055436dad9bc6e3a11f7cc.png)
azaz
![\[ \left(\frac{\partial \mu }{\partial p}\right)_T^\text{sz}< \left(\frac{\partial \mu }{\partial p}\right)_T^\text{foly}. \]](/images/math/c/0/f/c0f73f7b586e412b3b19bc3fde0e77a6.png)
Ez azt jelenti, hogy az előző feladatban felvázolt 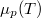 görbéből úgy kapjuk a nagyobb nyomáshoz tartozó görbét, ha minden egyes
görbéből úgy kapjuk a nagyobb nyomáshoz tartozó görbét, ha minden egyes  értékhez rendelt
értékhez rendelt 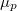 pontot megnövelünk egy állandó
pontot megnövelünk egy állandó 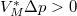 értékkel, de növelés mértéke a folyadék fázisban nagyobb, mint a szilárdban.
értékkel, de növelés mértéke a folyadék fázisban nagyobb, mint a szilárdban.
Látszik, hogy a két egyenes új metszéspontja 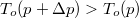 .
.
Víznél fagyáskor jelentős térfogatnövekedés lép fel, 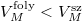 , ugyanezen szerkesztési menetet követve látható, hogy
, ugyanezen szerkesztési menetet követve látható, hogy 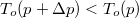 , azaz az új olvadáspont kisebb lesz.
, azaz az új olvadáspont kisebb lesz.