„Termodinamika példák - Fázisok egyensúlya szabadenergiával” változatai közötti eltérés
A Fizipedia wikiből
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
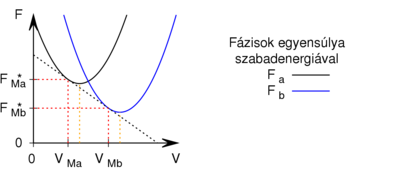
| − | </noinclude><wlatex># Egy homogén anyag adott hőmérsékleten két fázisban ($a$ és $b$) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.<br />Mutassuk ki, hogy egyensúlyi állapotban a fázisok $V_a$ és $V_b$ térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense! | + | </noinclude><wlatex># Egy homogén anyag adott hőmérsékleten két fázisban ($a$ és $b$) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.<br />Mutassuk ki, hogy egyensúlyi állapotban a fázisok $V_a$ és $V_b$ térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense![[Fájl:Fázisok egyensúlya szabadenergiával.svg|none|400px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=fejezzük ki a nyomást és a kémiai potenciált a szabad energiával ($p=-\partial F/\partial V$, ill. $\mu =\left(F+pV\right)/n$), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!}}</wlatex></includeonly><noinclude> |
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=fejezzük ki a nyomást és a kémiai potenciált a szabad energiával ($p=-\partial F/\partial V$, ill. $\mu =\left(F+pV\right)/n$), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!}}</wlatex></includeonly><noinclude> | + | |
== Megoldás == | == Megoldás == | ||
<wlatex>Egyensúlyban $p$, $T$, $\mu$ azonos a két fázisban. A szabadenergiára alkalmazható [[Termodinamika példák - A termodinamika differenciális összefüggései|differenciális összefüggés]]: | <wlatex>Egyensúlyban $p$, $T$, $\mu$ azonos a két fázisban. A szabadenergiára alkalmazható [[Termodinamika példák - A termodinamika differenciális összefüggései|differenciális összefüggés]]: | ||
| 30. sor: | 29. sor: | ||
* ha $V_{Ma}$ alatt van, csak az $a$ fázis lesz jelen | * ha $V_{Ma}$ alatt van, csak az $a$ fázis lesz jelen | ||
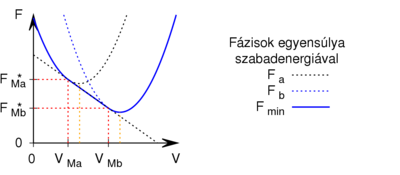
* ha $V_{Ma}$ felett és $V_{Mb}$ alatt van, mindkét fázis jelen lesz, az $a$ fázis $0<x<1$, a $b$ fázis $1-x$ részben alkotja a rendszert, hogy $x\cdot F_{Ma}^* + (1-x)\cdot F_{Mb}^* = F_{M}$ és $\frac{\textstyle V_{M}-V_{Mb}}{\textstyle V_{Ma}-V_{M}}=\frac{x}{1-x}$ | * ha $V_{Ma}$ felett és $V_{Mb}$ alatt van, mindkét fázis jelen lesz, az $a$ fázis $0<x<1$, a $b$ fázis $1-x$ részben alkotja a rendszert, hogy $x\cdot F_{Ma}^* + (1-x)\cdot F_{Mb}^* = F_{M}$ és $\frac{\textstyle V_{M}-V_{Mb}}{\textstyle V_{Ma}-V_{M}}=\frac{x}{1-x}$ | ||
| − | * ha $V_{Mb}$ felett van, csak a $b$ fázis lesz jelen | + | * ha $V_{Mb}$ felett van, csak a $b$ fázis lesz jelen. |
| + | [[Fájl:Fázisok egyensúlya szabadenergiával megjegyzés.svg|none|400px]] | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 21., 17:41-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy homogén anyag adott hőmérsékleten két fázisban (
 és
és  ) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
Mutassuk ki, hogy egyensúlyi állapotban a fázisok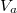 és
és 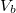 térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
Megoldás
Egyensúlyban  ,
,  ,
,  azonos a két fázisban. A szabadenergiára alkalmazható differenciális összefüggés:
azonos a két fázisban. A szabadenergiára alkalmazható differenciális összefüggés:
![\[ \left(\frac{\partial F}{\partial V}\right)_T = \left(\frac{\partial F_M}{\partial V_M}\right)_T = -p \]](/images/math/a/a/0/aa0c8c23937d7cc2dba2d2a86320ba66.png)
Mivel mindkét fázisban azonos a nyomás:
![\[ \left(\frac{\partial F_{Ma}}{\partial V_{M}}\right)_T = \left(\frac{\partial F_{Mb}}{\partial V_{M}}\right)_T = -p, \]](/images/math/8/b/4/8b49a47816bc9253795dde71ac955640.png)
azaz  és
és  fázis görbééin az egyensúly által kiválasztott egy-egy pont érintőinek a meredeksége azonos, a pontbeli érintők párhuzamosak.
fázis görbééin az egyensúly által kiválasztott egy-egy pont érintőinek a meredeksége azonos, a pontbeli érintők párhuzamosak.
Fejezzük ki a kémiai potenciált a megadott mennyiségekkel:
![\[ G=\mu n=F+pV, \qquad \mu = F_M+p V_M. \]](/images/math/5/f/e/5febb2b4e04b174c48515e7a01156f22.png)
Mivel mindkét fázisban azonos a kémiai potenciál és a nyomás:
![\[ -p = \frac{F_{Mb}- F_{Ma}}{V_{Mb}- V_{Ma}}, \]](/images/math/1/c/1/1c12a5029c560b385508da3697eb8873.png)
azaz  és
és  fázis görbéin az egyensúly által kiválasztott egy-egy pontot összekötő egyenes meredeksége is azonos kell legyen az előzőleg vizsgált két érintő egyenessel. Ezen három egyenes pedig csak a feladatban leírt esetben párhuzamosak.
fázis görbéin az egyensúly által kiválasztott egy-egy pontot összekötő egyenes meredeksége is azonos kell legyen az előzőleg vizsgált két érintő egyenessel. Ezen három egyenes pedig csak a feladatban leírt esetben párhuzamosak.
Megjegyzés
Egy kiválasztott 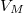 móltérfogat kijelöli az egyensúlyban a fázisok arányát:
móltérfogat kijelöli az egyensúlyban a fázisok arányát:
- ha
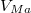 alatt van, csak az
alatt van, csak az  fázis lesz jelen
fázis lesz jelen
- ha
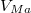 felett és
felett és 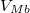 alatt van, mindkét fázis jelen lesz, az
alatt van, mindkét fázis jelen lesz, az  fázis
fázis 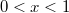 , a
, a  fázis
fázis 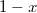 részben alkotja a rendszert, hogy
részben alkotja a rendszert, hogy 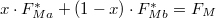 és
és 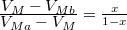
- ha
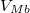 felett van, csak a
felett van, csak a  fázis lesz jelen.
fázis lesz jelen.