„Termodinamika példák - Hővezetés” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
a |
||
| 15. sor: | 15. sor: | ||
$$ \frac{\mathrm{d}Q}{\mathrm{d}t}=A\alpha \left(T-T_0\right). $$ | $$ \frac{\mathrm{d}Q}{\mathrm{d}t}=A\alpha \left(T-T_0\right). $$ | ||
| − | A test $\mathrm{d}T$ hőmérséklettel való hűlése $\mathrm{d}Q=-cm\,\mathrm{d}T$ hő elvonásával jár. A kapott | + | A test $\mathrm{d}T$ hőmérséklettel való hűlése $\mathrm{d}Q=-cm\,\mathrm{d}T$ hő elvonásával jár. A kapott |
$$ -\frac{cm\,\mathrm{d}T}{\mathrm{d}t} = A\alpha \left(T-T_0\right), $$ | $$ -\frac{cm\,\mathrm{d}T}{\mathrm{d}t} = A\alpha \left(T-T_0\right), $$ | ||
| − | az eredményt a $T(0)=T_1$ kezdeti feltételre illesztve | + | differenciálegyenlet a változók szétválasztásának módszerével megoldható, az eredményt a $T(0)=T_1$ kezdeti feltételre illesztve |
$$ \ln \left(\frac{T-T_0}{T_1-T_0}\right) = \frac{A\alpha}{cm}t.$$ | $$ \ln \left(\frac{T-T_0}{T_1-T_0}\right) = \frac{A\alpha}{cm}t.$$ | ||
| − | + | A test pillanatnyi hőmérséklete: | |
$$ T = T_0+\left(T_1-T_0\right)e^{\textstyle -\frac{A\alpha}{cm}t}. $$ | $$ T = T_0+\left(T_1-T_0\right)e^{\textstyle -\frac{A\alpha}{cm}t}. $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 27., 11:12-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
hőmérsékletű, igen nagy hőkapacitású folyadékba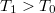 
hőmérsékletű, 
tömegű és 
fajhőjű, abszolút jó hővezető testet helyezünk a 
pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik (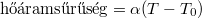
), az 
hőátadási tényező ismert, a test felületének nagysága 
. Határozzuk meg a test hőmérsékletét 
idő eltelte után!
Megoldás
Hővezetés alapegyenlete a Newton-féle lehűlési törvénnyel:
![\[ \frac{\mathrm{d}Q}{\mathrm{d}t}=A\alpha \left(T-T_0\right). \]](/images/math/a/3/8/a38ca252ca63b5b48ab51d4159278bc0.png)
A test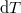 
hőmérséklettel való hűlése 
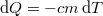hő elvonásával jár. A kapott
![\[ -\frac{cm\,\mathrm{d}T}{\mathrm{d}t} = A\alpha \left(T-T_0\right), \]](/images/math/4/6/5/46500fa8d5545c2320e160c7d0a994e4.png)
differenciálegyenlet a változók szétválasztásának módszerével megoldható, az eredményt a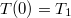 
kezdeti feltételre illesztve
![\[ \ln \left(\frac{T-T_0}{T_1-T_0}\right) = \frac{A\alpha}{cm}t.\]](/images/math/0/4/4/044a8ec808c9a64316a466b7e63c5764.png)
A test pillanatnyi hőmérséklete:
![\[ T = T_0+\left(T_1-T_0\right)e^{\textstyle -\frac{A\alpha}{cm}t}. \]](/images/math/5/6/0/560d55d23061281178ad6c229fe22185.png)
