„Termodinamika példák - Ideális gáz kompresszibilitásai” változatai közötti eltérés

A Fizipedia wikiből
a (→‎Megoldás)
a (Szöveg koherenssé tétele)
 
13. sor: 13. sor:
 
== Megoldás ==
 
== Megoldás ==
 
<wlatex>A kompresszibilitás '''általános''' definíciója
 
<wlatex>A kompresszibilitás '''általános''' definíciója
−
$${\kappa }_{\star}=-\frac{1}{V} \left(\frac{\partial V}{\partial p}\right)_{\star},$$
+
$$ {\kappa }_{\substack{\text{állapot-}\\ \text{változás}}} = -\frac{1}{V} \left(\frac{\partial V}{\partial p}\right)_{\substack{\text{állapot-}\\ \text{változás}}},$$
−
ahol a $\star$ arra utal, hogy iránymenti deriváltat kell képezni az állapotváltozás egyenlete által meghatározott vonalon.
+
ahol iránymenti deriváltat kell képezni az állapotváltozás egyenlete által meghatározott vonalon.
  
−
'''Izoterm''' esetben az állapotegyenletből $$V(p)=NkT\cdot\frac{1}{p},$$
+
'''Izoterm''' esetben az állapotegyenlet
−
amiből $$\left(\frac{\mathrm{d}V}{\mathrm{d}p}\right)_T=-\frac{NkT}{p^2}=-\frac{V}{p},$$
+
$$V(p) = NkT\cdot\frac{1}{p}, $$
−
azaz az izoterm kompresszibilitás $$\kappa_T=\frac{1}{p}$$
+
amiből
 +
$$ \left(\frac{\mathrm{d}V}{\mathrm{d}p}\right)_T = -\frac{NkT}{p^2}=-\frac{V}{p}, $$
 +
azaz az izoterm kompresszibilitás
 +
$$ \kappa_T = \frac{1}{p}. $$
  
 
'''Adiabatikus''' esetben az adiabata egyenletének egyik alakjából kell kiindulnunk:
 
'''Adiabatikus''' esetben az adiabata egyenletének egyik alakjából kell kiindulnunk:
−
* $p V^\gamma = \mathrm{const.} $ egyenletet $V$ szerint deriválva
+
$p V^\gamma = \mathrm{const.} $ egyenletet $V$ szerint deriválva
 
$$ \frac{\mathrm{d}p}{\mathrm{d}V}V^\gamma + \gamma p V^{\gamma-1} = 0, $$
 
$$ \frac{\mathrm{d}p}{\mathrm{d}V}V^\gamma + \gamma p V^{\gamma-1} = 0, $$
 
amiből
 
amiből
 
$$ \frac{\mathrm{d}p}{\mathrm{d}V} = -\frac{\gamma p}{V},$$
 
$$ \frac{\mathrm{d}p}{\mathrm{d}V} = -\frac{\gamma p}{V},$$
−
aminek formálisan vehetjük a reciprokát, ha továbbra is az adiabata mentén számítjuk_
+
aminek formálisan vehetjük a reciprokát, ha továbbra is az adiabata mentén számítjuk:
−
$$ -\frac{1}{V}\frac{\mathrm{d}V}{\mathrm{d}p} = \frac{1}{\gamma p}.$$
+
$$ \kappa_\text{ad} = -\frac{1}{V}\frac{\mathrm{d}V}{\mathrm{d}p} = \frac{1}{\gamma p}.$$
  
−
* $p V^\gamma = \mathrm{const.} $ egyenletet $p$ szerint deriválva
+
== Megjegyzés ==
 +
'''Adiabatikus''' esetben a $p V^\gamma = \mathrm{const.} $ egyenletet $p$ szerint deriválva
 
$$ V^\gamma+\gamma p V^{\gamma-1}\frac{\mathrm{d}V}{\mathrm{d}p} = 0, $$
 
$$ V^\gamma+\gamma p V^{\gamma-1}\frac{\mathrm{d}V}{\mathrm{d}p} = 0, $$
 
ami ismét az előző eredményre vezet:
 
ami ismét az előző eredményre vezet:
−
$$\kappa_{\text{ad}}=\frac{1}{\gamma p}.$$
+
$$ \kappa_\text{ad} = \frac{1}{\gamma p}. $$
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2013. április 28., 16:53-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Állapotváltozás, I. főtétel
Feladatok listája:
  1. Állapotváltozások diagramjai
  2. Belső energia állapotváltozásokban
  3. Energiák fajhőviszonnyal
  4. Energiaváltozások diagramból
  5. Ideális gáz kompresszibilitásai
  6. Nyomás hőmérsékletfüggése
  7. Fűtött szoba belső energiája
  8. Térfogatváltozás fajhőviszonnyal
  9. Van der Waals-gáz egyensúlya
  10. Közelítő állapotegyenlet
  11. Állapotegy. mérh. menny.-ből
  12. Van der Waals-gáz fajhőkülönbsége
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

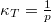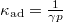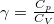  1. Mutassa meg, hogy ideális gáz izoterm összenyomásánál a kompresszibilitás \setbox0\hbox{$\kappa_T=\frac1p$}% \message{//depth:\the\dp0//}% \box0%, míg adiabatikus összenyomásnál \setbox0\hbox{$\kappa_{\text{ad}}=\frac{1}{\gamma p}$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$\gamma =\frac{C_p}{C_V}$}% \message{//depth:\the\dp0//}% \box0%.

Megoldás

A kompresszibilitás általános definíciója

\[ {\kappa }_{\substack{\text{állapot-}\\ \text{változás}}} = -\frac{1}{V} \left(\frac{\partial V}{\partial p}\right)_{\substack{\text{állapot-}\\ \text{változás}}},\]

ahol iránymenti deriváltat kell képezni az állapotváltozás egyenlete által meghatározott vonalon.

Izoterm esetben az állapotegyenlet

\[V(p) = NkT\cdot\frac{1}{p}, \]

amiből

\[ \left(\frac{\mathrm{d}V}{\mathrm{d}p}\right)_T = -\frac{NkT}{p^2}=-\frac{V}{p}, \]

azaz az izoterm kompresszibilitás

\[ \kappa_T = \frac{1}{p}. \]

Adiabatikus esetben az adiabata egyenletének egyik alakjából kell kiindulnunk: 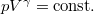\setbox0\hbox{$p V^\gamma = \mathrm{const.} $}% \message{//depth:\the\dp0//}% \box0% egyenletet \setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0% szerint deriválva

\[ \frac{\mathrm{d}p}{\mathrm{d}V}V^\gamma + \gamma p V^{\gamma-1} = 0, \]

amiből

\[ \frac{\mathrm{d}p}{\mathrm{d}V} = -\frac{\gamma p}{V},\]

aminek formálisan vehetjük a reciprokát, ha továbbra is az adiabata mentén számítjuk:

\[ \kappa_\text{ad} = -\frac{1}{V}\frac{\mathrm{d}V}{\mathrm{d}p} = \frac{1}{\gamma p}.\]

Megjegyzés

Adiabatikus esetben a 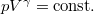\setbox0\hbox{$p V^\gamma = \mathrm{const.} $}% \message{//depth:\the\dp0//}% \box0% egyenletet \setbox0\hbox{$p$}% \message{//depth:\the\dp0//}% \box0% szerint deriválva

\[ V^\gamma+\gamma p V^{\gamma-1}\frac{\mathrm{d}V}{\mathrm{d}p} = 0, \]

ami ismét az előző eredményre vezet:

\[ \kappa_\text{ad} = \frac{1}{\gamma p}. \]
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_Ideális_gáz_kompresszibilitásai&oldid=9604”