Termodinamika példák - Jég olvadáshőjének becslése
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. május 28., 22:24-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- A jég olvadáshője
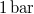 nyomáson
nyomáson 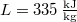 . A jég és a víz fajlagos térfogatának aránya
. A jég és a víz fajlagos térfogatának aránya 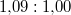 . Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
Megoldás
Alkalmazzuk a Clapeyron-egyenlet
![\[ \mathrm{d}T = \frac{T\Delta V_M}{L_M}\,\mathrm{d}p \]](/images/math/1/c/9/1c9a928d4df240fee8dd8ba16af94782.png)
alakját az olvadásra. Tudjuk, hogy
![\[ \frac{\Delta V_M}{L_{M\,\text{olv}}} = \frac{\Delta v}{L_\text{olv}}, \]](/images/math/6/9/6/6969c59bcea6caac13edf0cdf75351c3.png)
hiszen a moláris mennyiségeket egységnyi tömegre bővíthetjük. A fázisátalakulásban a jeget tekintjük kezdeti, a vizet végállapotnak (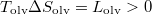 ):
):
![\[ \Delta v = (1{,}00-1{,}09) v_\text{víz}, \]](/images/math/9/7/b/97bfcff34c31800e8332d9acdce93aaf.png)
hiszen a víz 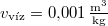 fajlagos térfogatát adták meg referenciaként. A jég olvadáshője
fajlagos térfogatát adták meg referenciaként. A jég olvadáshője 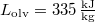 , olvadáspontja
, olvadáspontja 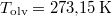 , amivel
, amivel
![\[ \mathrm{d}T = -\frac{0{,}09v_\text{víz}T_\text{olv}}{L_\text{olv}}\,\mathrm{d}p = -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p. \]](/images/math/2/8/5/285302e1fd5d53432663024f5c7d6639.png)