Termodinamika példák - Termodinamikai potenciálok víz elforralásakor

Feladat

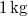1. $\setbox0\hbox{$1\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ víznek normál nyomáson (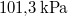$\setbox0\hbox{$101{,}3\,\mathrm{kPa}$}% \message{//depth:\the\dp0//}% \box0%$) való elforralásához egy elektromos merülőforralón a 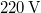$\setbox0\hbox{$220\,\mathrm{V}$}% \message{//depth:\the\dp0//}% \box0%$-os feszültségforrásból 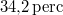$\setbox0\hbox{$34{,}2\,\mathrm{perc}$}% \message{//depth:\the\dp0//}% \box0%$-en át 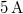$\setbox0\hbox{$5\,\mathrm{A}$}% \message{//depth:\the\dp0//}% \box0%$ áramot kell átfolyatni. A gázállandó 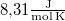$\setbox0\hbox{$8{,}31\mathrm{\frac{J}{mol\,K}}$}% \message{//depth:\the\dp0//}% \box0%$, a víz moláris tömege $\setbox0\hbox{$18{,}01528\,\mathrm{\frac{g}{mol}}$}% \message{//depth:\the\dp0//}% \box0%$.
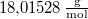   Határozzuk meg a víz
   • a) entalpia-,
   • b) entrópia- és
   • c) belső energiaváltozását ebben a folyamatban!

Megoldás

Az elforralás állandó (légköri) nyomáson és állandó (forrásponti) hőmérsékleten zajlik.

a) Az átalakulási hőről szóló feladat alapján az eltalpiaváltozás az álladó nyomáson vett átalakulási hő, ez pedig a befektetett elektromos munka:

$\[ \Delta H = \Delta Q = W_\text{el} = U_0 I_0 \Delta t \approx 2\,257\,\mathrm{kJ}. \]$

b) Mivel a hőmérséklet állandó, az entrópiaváltozást definiáló integrál leegyszerűsödik:

$\[ \Delta S = \int_\text{kezd}^\text{vég} \mathrm{d}S = \int_{\substack{\text{átala-}\\ \text{kulás}}} \frac{\delta Q}{T} = \frac{\Delta Q}{T}\approx 6\,051 \mathrm{\frac{J}{K}}. \]$

c) Az első főtétel alapján álladó nyomáson

$\[ \Delta U=\Delta Q-p\Delta V, \]$

ahol a térfogatváltozás számításánál a gőzt mint ideális gázt tekintjük, és térfogatához képest a folyadék térfogatát elhanyagolhatjuk (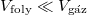$\setbox0\hbox{$V_\text{foly}\ll V_\text{gáz}$}% \message{//depth:\the\dp0//}% \box0%$):

$\[ \Delta V = V_\text{gőz}-V_\text{víz} \approx V_\text{gőz} = \frac{m}{M}\frac{RT}{p}, \]$

így a belső energia megváltozása

$\[ \Delta U = \Delta Q-\frac{m}{M}RT = 2\,085\,\mathrm{kJ}. \]$