Termodinamika példák - Ideális gáz kompresszibilitásai

Feladat

1. Mutassa meg, hogy ideális gáz izoterm összenyomásánál a kompresszibilitás 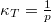$\setbox0\hbox{$\kappa_T=\frac1p$}% \message{//depth:\the\dp0//}% \box0%$, míg adiabatikus összenyomásnál 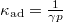$\setbox0\hbox{$\kappa_{\text{ad}}=\frac{1}{\gamma p}$}% \message{//depth:\the\dp0//}% \box0%$, ahol $\setbox0\hbox{$\gamma =\frac{C_p}{C_V}$}% \message{//depth:\the\dp0//}% \box0%$.

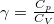Megoldás

A kompresszibilitás általános definíciója

$\[{\kappa }_{\star}=-\frac{1}{V} \left(\frac{\partial V}{\partial p}\right)_{\star},\]$

ahol a $\setbox0\hbox{$\star$}% \message{//depth:\the\dp0//}% \box0%$ arra utal, hogy iránymenti deriváltat kell képezni az állapotváltozás egyenlete által meghatározott vonalon.

Izoterm esetben az állapotegyenletből

$\[V(p)=NkT\cdot\frac{1}{p},\]$

amiből

$\[\left(\frac{\mathrm{d}V}{\mathrm{d}p}\right)_T=-\frac{NkT}{p^2}=-\frac{V}{p},\]$

azaz az izoterm kompresszibilitás

$\[\kappa_T=\frac{1}{p}\]$

Adiabatikus esetben az adiabata egyenletének egyik alakjából kell kiindulnunk:

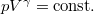• $\setbox0\hbox{$p V^\gamma = \mathrm{const.} $}% \message{//depth:\the\dp0//}% \box0%$ egyenletet $\setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0%$ szerint deriválva

$\[ \frac{\mathrm{d}p}{\mathrm{d}V}V^\gamma + \gamma p V^{\gamma-1} = 0, \]$

amiből

$\[ \frac{\mathrm{d}p}{\mathrm{d}V} = -\frac{\gamma p}{V},\]$

aminek formálisan vehetjük a reciprokát, ha továbbra is az adiabata mentén számítjuk_

$\[ -\frac{1}{V}\frac{\mathrm{d}V}{\mathrm{d}p} = \frac{1}{\gamma p}.\]$

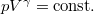• $\setbox0\hbox{$p V^\gamma = \mathrm{const.} $}% \message{//depth:\the\dp0//}% \box0%$ egyenletet $\setbox0\hbox{$p$}% \message{//depth:\the\dp0//}% \box0%$ szerint deriválva

$\[ V^\gamma+\gamma p V^{\gamma-1}\frac{\mathrm{d}V}{\mathrm{d}p} = 0, \]$

ami ismét az előző eredményre vezet:

$\[\kappa_{\mathit{ad}}=\frac{1}{\gamma p}.\]$