Termodinamika példák - Gázcsere két gázzal

Feladat

1. Két azonos térfogatú tartály kacsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben 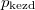$\setbox0\hbox{$p_\text{kezd}$}% \message{//depth:\the\dp0//}% \box0%$ nyomású hidrogéngáz, a másikban kétszer akkora nyomású oxigéngáz van. A gázok $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$ hőmérséklete azonos és időben állandó. 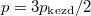A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos $\setbox0\hbox{$p=3p_\text{kezd}/2$}% \message{//depth:\the\dp0//}% \box0%$ egyensúlyi nyomás alakul ki!

Megoldás

A gázcsere kis lyukon keresztül valósul meg a tartályok között, feltehetjük, hogy a gáz egy-egy tartályon belül végig egyensúlyi állapotban marad. Ha a lyuk mérete sokkal kisebb az átlagos szabad úthossznál, akkor a rajta keresztül időegység alatt távozó molekulák száma megegyezik azzal, amit a gáz kinetikus elméletében a nyomás tárgyalásakor a tartály falának ugyanakkora felületét időegység alatt érő molekulák számára kapunk (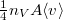$\setbox0\hbox{$\frac14 n_V A \langle v \rangle$}% \message{//depth:\the\dp0//}% \box0%$). Ideális gázok molekulái sem saját fajtájukkal, sem a másik gázzal nem hatnak kölcsön, ezért külön differenciálegyenleteket írhatunk fel az egyes gázokra:

$\[ \frac{\mathrm{d}N^{(1)}_H}{\mathrm{d}t} = - \frac14 n_{VH}^{(1)}\langle v_H \rangle A + \frac14 n_{VH}^{(2)}\langle v_H \rangle A = \frac14 \langle v_H \rangle A \left(n_{VH}^{(2)}-n_{VH}^{(1)}\right),\]$

$\[ \frac{\mathrm{d}N^{(1)}_O}{\mathrm{d}t} = - \frac14 n_{VO}^{(1)}\langle v_O \rangle A + \frac14 n_{VO}^{(2)}\langle v_O \rangle A = \frac14 \langle v_O \rangle A \left(n_{VO}^{(2)}-n_{VO}^{(1)}\right),\]$

a molekulák átlagos sebessége 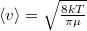$\setbox0\hbox{$\langle v \rangle = \sqrt{\frac{8kT}{\pi \mu }}$}% \message{//depth:\the\dp0//}% \box0%$ fordítottan arányos a $\setbox0\hbox{$\mu$}% \message{//depth:\the\dp0//}% \box0%$ molekulatömeggel (a két tartály hőmérséklete azonos): $\setbox0\hbox{$\mu_{H_2}=2\,\mathrm{\frac{g}{mol}}$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$\mu_{O_2}=32\,\mathrm{\frac{g}{mol}}$}% \message{//depth:\the\dp0//}% \box0%$. 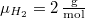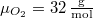Az anyagmegmaradás következtében a 2. tartály tartalmát nem kell külön számon tartanunk.

Legyen kezdetben az 1. tartályban a hidrogén és a 2.-ban az oxigén:

$\[ n_{VH\text{kezd}}^{(1)} = n_{VH\text{kezd}}, \qquad n_{VH\text{kezd}}^{(2)}=0, \]$

$\[ n_{VO\text{kezd}}^{(2)} = n_{VO\text{kezd}}, \qquad n_{VO\text{kezd}}^{(1)}=0. \]$

Egyensúlyban 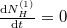$\setbox0\hbox{$\frac{\mathrm{d}N^{(1)}_H}{\mathrm{d}t}=0$}% \message{//depth:\the\dp0//}% \box0%$, azaz $\setbox0\hbox{$n_{VH\text{vég}}^{(1)}=n_{VH\text{vég}}^{(2)}=n_{VH\text{vég}}$}% \message{//depth:\the\dp0//}% \box0%$.

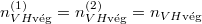Az anyagmegmaradás értelmében 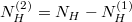$\setbox0\hbox{$N_H^{(2)}=N_H-N_H^{(1)}$}% \message{//depth:\the\dp0//}% \box0%$:

$\[ V^{(1)} n_{VH} = V^{(1)} n_{VH}^{(1)} + V^{(2)} n_{VH}^{(2)} = n_{VH\text{vég}} \left( V^{(1)} + V^{(2)} \right), \]$

az a kezdeti feltételeket behelyettesítve a hidrogénre és analóg módon az oxigénre

$\[ n_{VH\text{vég}} = \frac{V^{(1)}}{V^{(1)} + V^{(2)}} n_{VH\text{kezd}}, \]$

$\[ n_{VO\text{vég}} = \frac{V^{(2)}}{V^{(1)} + V^{(2)}} n_{VO\text{kezd}}. \]$

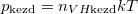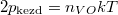A kezdeti $\setbox0\hbox{$p_\text{kezd} = n_{VH\text{kezd}}kT$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$2p_\text{kezd} = n_{VO}kT$}% \message{//depth:\the\dp0//}% \box0%$ nyomásokból 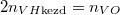$\setbox0\hbox{$2n_{VH\text{kezd}}=n_{VO}$}% \message{//depth:\the\dp0//}% \box0%$ összefüggést nyerjük. A kialakuló

$\[ p_{O\text{vég}} = n_{VO\text{vég}}kT = \frac{V^{(2)}}{V^{(1)}+V^{(2)}} 2p_\text{kezd}, \]$

$\[ p_{H\text{vég}} = n_{VH\text{vég}}kT = \frac{V^{(1)}}{V^{(1)}+V^{(2)}} p_\text{kezd} \]$

nyomásokból pedig a parciális nyomások tétele (Dalton-törvény) szerint

$\[ p_\text{vég} = p_{H\text{vég}} + p_{O\text{vég}} = \left(\frac{2V^{(2)}}{V^{(1)}+V^{(2)}} + \frac{V^{(1)}}{V^{(1)}+V^{(2)}}\right) p_\text{kezd}\]$

adódik.

Speciálisan a feladatban 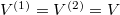$\setbox0\hbox{$V^{(1)}=V^{(2)}=V$}% \message{//depth:\the\dp0//}% \box0%$, (továbbá 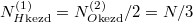$\setbox0\hbox{$N_{H\text{kezd}}^{(1)}=N_{O\text{kezd}}^{(2)}/2=N/3$}% \message{//depth:\the\dp0//}% \box0%$), így a kialakuló egyensúlyi nyomás $\setbox0\hbox{$p=3p_\text{kezd}/2$}% \message{//depth:\the\dp0//}% \box0%$.

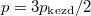A részecskeszámokra vonatkozó differenciálegyenletek megoldása az előző feladatéval analóg.