Magnetosztatika példák - Egyenes vezető mágneses tere 2
Feladat
Határozzuk meg egy végtelen hosszú egyenes vezető mágneses terét, mint a vezetőtől mért távolság függvényét! A vezetőben  áram folyik. A számításokat végezzük az Amper-féle gerjesztési törvény segítségével!
áram folyik. A számításokat végezzük az Amper-féle gerjesztési törvény segítségével!
Megoldás
Végtelen hosszú vezető esetén az Egyenes vezető mágneses tere feladatában szereplő Biot-Savart törvény nehézkes integrálását kiválthatjuk az Amper-féle gerjesztési törvény alkalmazásával. Ilyenkor kihasználjuk, hogy a rendszer hengerszimmetrikus, továbbá a vezető tengelye mentén eltolási szimmetriával rendelkezik. Felveszünk egy  sugarú gyűrűt, melynek síkja merőleges a vezetékre, tengelye pedig azzal egybe esik. A gyűrűre, mint zárt görbére felírjuk az Amper-féle gerjesztési törvényt:
sugarú gyűrűt, melynek síkja merőleges a vezetékre, tengelye pedig azzal egybe esik. A gyűrűre, mint zárt görbére felírjuk az Amper-féle gerjesztési törvényt:
![\[I=\oint \overline{Hdl}\]](/images/math/b/2/6/b26c7cf6f7513450d437b66a558e3671.png)
Ahol  a gyűrű által bezárt területen átfolyó áramerősség (megegyezik a vezetékben folyó árammal),
a gyűrű által bezárt területen átfolyó áramerősség (megegyezik a vezetékben folyó árammal),  pedig a gyűrű alakú görbe egyes pontjaiban mérhető mágneses térerősség. Tekintve, hogy a rendszer hengerszimmetrikus, a mágneses teret is hengerszimmetrikusnak feltételezhetjük, mely örvényesen veszi körül a vezetéket. Iránya mindenütt párhuzamos a gyűrű
pedig a gyűrű alakú görbe egyes pontjaiban mérhető mágneses térerősség. Tekintve, hogy a rendszer hengerszimmetrikus, a mágneses teret is hengerszimmetrikusnak feltételezhetjük, mely örvényesen veszi körül a vezetéket. Iránya mindenütt párhuzamos a gyűrű  ívelemével. Emiatt az Amper-féle gerjesztési törvényben szereplő vektorok skalárszorzata egyszerűsíthető a mennyiségek skaláris értékeinek szorzatával:
ívelemével. Emiatt az Amper-féle gerjesztési törvényben szereplő vektorok skalárszorzata egyszerűsíthető a mennyiségek skaláris értékeinek szorzatával:
![\[I=\oint Hdl\]](/images/math/2/0/3/20384c54ae52e0a04bf8df8506b7fdd2.png)
Ugyancsak a hengerszimmetria miatt feltételezzük, hogy a gyűrű mentén mindenütt konstans  nagyságú tér merhető. Az integrál tovább egyszerűsödik:
nagyságú tér merhető. Az integrál tovább egyszerűsödik:
![\[I=H\oint dl=2r\pi H\]](/images/math/1/4/c/14c1066f4efb43b1cf9fc43b14b1015b.png)
Hiszen a fenti körintegrál a gyűrű kerületét adja meg.
Ebből kifejezve a mágneses teret:
![\[H= \dfrac{I}{2\pi r}\]](/images/math/8/c/c/8cc5ebc11a83bc0e7312819cb579b75b.png)
Az indukció ennek 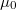 -szorosa:
-szorosa:
![\[B= \dfrac{\mu_0 I}{2\pi r}\]](/images/math/f/1/0/f10fdea2c59fc782f76c37e7ede59acd.png)