| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Magnetosztatika - Biot-Savart törvény, gerjesztési törvény
|
Feladatok listája:
- Egyenes vezető mágneses tere
- Egyenes vezető mágneses tere 2
- Áram által átjárt vezető elrendezés mágneses tere
- Áram által átjárt hengeres vezetékben a mágneses tér
- Áram által átjárt üreges hengerben a mágneses tér
- Párhuzamos, végtelen vezetők mágneses tere
- Gyűrű alakú vezető mágneses tere
- Négyzet alakú fémkeret mágneses tere
- Koaxiális vezető mágneses tere
- Körív alakú vezető mágneses tere
- Körmozgást végző töltött test mágneses tere
- Forgó korong mágneses tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Határozzuk meg az áramvonalak törési törvényét a
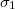 és
és 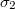 vezetőképességű közegek határán.
vezetőképességű közegek határán.
Megoldás
Legyen 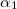 és
és 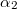 az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
Az örvénymentességből pedig következik, hogy az elektromos tér felületre párhuzamos komponense folytonosan megy át:
Ebbe a differenciális Ohm-törvényt beírva:
A kapott két egyenletet elosztva, kiesik az áramsűrűség, és azt kapjuk:
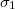 és
és 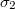 vezetőképességű közegek határán.
vezetőképességű közegek határán.
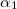 és
és 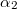 az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
az áramvonalaknak a merőlegessel bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
![\[\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) \]](/images/math/8/2/7/827afd735af94c884dc0fc233fb2b9ca.png)
![\[E_{1t} = E_{2t} \]](/images/math/d/5/9/d59760c33230de53eb5d60da46323704.png)
![\[\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}\]](/images/math/0/2/9/029ee907ef9cee8ec9ebb36074712905.png)
![\[\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)\]](/images/math/a/9/b/a9b91a5d5a4e80746e75088230a80969.png)