Magnetosztatika példák - Párhuzamos, végtelen vezetők mágneses tere
Feladat
Két egymással párhuzamos, végtelen hosszú 
sugarú hengeres vezetőben 
erősségű áram folyik azonos irányba, az ábra síkjára merőlegesen befelé. A hengerek tengelytávolsága 
. Az áramsűrűség a vezetők keresztmetszetén állandó. Mekkora a 
mágneses indukció az ábrán jelölt 
, , 
és pontokban? (abra)
Megoldás
A szuperpozíció elvéből következik, hogy a két végtelen vezető henger tere megegyezik az egyes vezető hengerek által keltett terek összegével. A 6. feladatsor 4. feladatából jól ismerjük a végtelen hosszú, árammal átjárt vezető henger mágneses terének nagyságát a tengelytől mért 
távolság függvényében:
kívül:
![\[B_{(r)}=\dfrac{\mu_0 I}{2\pi r}\]](/images/math/e/1/9/e19d8fa41e8b66fef89e955cdafc2ca6.png)
és belül:
![\[B_{(r)}=\dfrac{\mu_0 jr}{2}\]](/images/math/1/8/c/18c58287ed343f1a1204d51ad2358851.png)
A hengerben folyó egyenletes áramsűrűség nagysága:
![\[j=\dfrac{I}{R^2\pi}\]](/images/math/4/f/1/4f1fce5c695e0396a6edf5ba68380f75.png)
Így a tér nagysága a henger belsejében a jelen feladatban megadott mennyiségekkel:
![\[B_{(r)}=\dfrac{\mu_0 Ir}{2\pi R^2}\]](/images/math/c/f/9/cf95358bc7630645b00e5afd2eb64260.png)
Az egyes hengeres vezetők által keltett tér az óramutató járásával azonos irányban, körkörösen veszi körbe a hengerek tengelyét.
A)
A fentiek alapján könnyen belátható, hogy a két henger szimmetriapontjában az egyes hengerek által keltett terek nagysága megegyezik, irányuk pedig ellentétes, tehát kioltják egymást:
![\[B_A=0\]](/images/math/5/2/4/5249640f86be299e615d5ebf267ff07f.png)
B)
A B pont az egyik henger tengelyén helyezkedik el, tehát ott teret csak a másik hengerben folyó áram kelthet. Ennek nagysága:
![\[B_B=\dfrac{\mu_0 I}{2\pi d}\]](/images/math/8/9/a/89a5e86989870e8ddb76e3ba252c9e22.png)
Iránya pedig az ábrán 'felfelé' mutat.
C)
A C pontban az első henger 'lefelé' irányuló,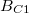 
nagyságú teret kelt:
![\[B_{C1}=\dfrac{\mu_0 I}{2\pi \left( d-\dfrac{R}{2}\right)}\]](/images/math/3/b/d/3bddd7afb5c0565137ea80d7900ccb35.png)
A második henger járuléka 'felfelé' mutató vektor, nagysága:
![\[B_{C1}=-\dfrac{\mu_0 I}{2\pi R^2}\dfrac{R}{2}=-\dfrac{\mu_0 I}{4\pi R}\]](/images/math/f/2/6/f26eed5d81edc66d946d00f1743d593e.png)
Tehát az eredő tér a C pontban:
![\[B_{C}=B_{C1}+B_{C2}=\dfrac{\mu_0 I}{2\pi \left( d-\dfrac{R}{2}\right)}-\dfrac{\mu_0 I}{4\pi R}= \dfrac{\mu_0 I}{2\pi} \left( \dfrac{1}{ d-\dfrac{R}{2}}-\dfrac{1}{2 R} \right)\]](/images/math/d/6/1/d6119b421afeee0a43f35ab08493c7c5.png)
