Magnetosztatika példák - Körmozgást végző töltött test mágneses tere
Feladat
hosszúságú szigetelőpálca végére elhelyezett kisméretű testet 
töltéssel látunk el. A szigetelő nyél másik végét tengelyhez rögzítve 
szögsebességgel megforgatjuk.
a) Milyen hatással lesz a körmozgást végző töltött test a környezetére?
b) Mekkora és milyen irányú lesz a mágneses indukció a kör középpontján átmenő, pálya síkjára merőleges tengely mentén?
Megoldás
a.) A körmozgást végző töltés jó közelítéssel köráramnak tekinthető. Az áram erőssége:
![\[I=\dfrac{\Delta Q}{\Delta t}\]](/images/math/e/e/a/eea40355d458766514c9b89041deedb4.png)
Ahol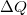 
a körpálya adott pontján 
idő alatt áthaladt töltések mennyisége. Tekintve, hogy a ponttöltés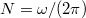 
fordulatszámmal kering:
![\[I=\dfrac{\Delta Q}{\Delta t}=\dfrac{QN \Delta t}{\Delta t}=\dfrac{Q\omega}{2\pi}\]](/images/math/6/9/8/6988dfa2fe80767aefb7fcf889856ca4.png)
b.) Feladatunk tehát egy fent meghatározott 
áramerősségű, sugarú körvetető terének meghatározása a tengely mentén, a köráram síkjától 
távolságban. A Biot-Savart törvényt fogjuk alkalmazni:
![\[\vec{B}=\dfrac{\mu_0 I}{4 \pi} \int \dfrac{\vec{dl}\times \vec{r}}{|r|^3}\]](/images/math/8/2/3/8235c45413b85686886646b1d0247c04.png)
A vizsgált tengelypontból a körvezető adott infinitezimális 
szakaszához húzott 
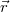sugarak egy magasságú kúpot határoznak meg az ábra szerint.
ábra
Mivel a kúp 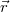alkotói mindig merőlegesek a körvezető 
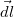érintőire, a Biot-Savart törvény alapján egy elemi hosszúságú vezetékdarab által vizsgált pontban keltett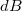 
indukció komponens nagysága a következőképp alakul:
![\[dB=\dfrac{\mu_0 I}{4 \pi} \dfrac{dl}{r^2}\]](/images/math/4/e/7/4e795ff647e1b3d44af98f28fb4d14ee.png)
A 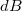elemi indukció vektor merőleges az őt keltő 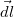vezető darabra, és a hozzá vezető 
alkotóra. A rendszer hengerszimmetriája miatt feltételezhetjük, hogy a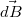 
vektorok vízszintes komponensei kioltják egymást, a függőleges komponensek viszont konstruktívan összegződnek. A merőleges szárú szögek tétele alapján beláthatjuk, hogy 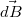vektor a vízszintessel 
szöget zár be, ahol a kúp alkotója és forgástengelye által bezárt szög. Geometriai megfontolások alapján:
![\[\sin(\beta)=\dfrac{R}{r}\]](/images/math/d/c/c/dcc485ad353e75ee96c1924b9b53ef1a.png)
Tehát a 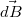függőleges komponense:
![\[dB_z=dB\sin(\beta)=\dfrac{\mu_0 I}{4 \pi} \dfrac{dl}{r^2}\dfrac{R}{r}=\dfrac{\mu_0 I R}{4 \pi r^3} dl\]](/images/math/7/4/c/74c12652e5d981245a9d587e8f24f76b.png)
Ahol a vezető elemi szakaszdarabja parametrizálható a az infinitezimális ívelem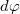 
középponti szögével:
![\[dl=Rd\varphi\]](/images/math/3/1/a/31a804f711a1b070a6143e68d4d7c0e5.png)
![\[dB_z=\dfrac{\mu_0 I R^2}{4 \pi r^3} d\varphi\]](/images/math/5/7/9/579a246c3e888080e4aceac09e35679b.png)
Az teljes gyűrű által keltett mágneses indukciót meghatározhatjuk, ha a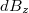 
járulékokat felösszegezzük a gyűrű teljes körére:
![\[B_z=\int dB_z=\dfrac{\mu_0 I R^2}{4 \pi r^3} \int_0^{2\pi} d\varphi=\dfrac{\mu_0 I R^2}{4 \pi r^3}2\pi=\dfrac{\mu_0 I R^2}{2 r^3}\]](/images/math/0/4/d/04d4041805a08484df32b4fc697f552e.png)
Kihasználva, hogy:
![\[r^2=R^2+z^2\]](/images/math/2/2/6/2265ac4232bb27d24358128c06d0dbbe.png)
Az indukció nagysága a függvényében:
![\[B_z=\dfrac{\mu_0 I R^2}{2 (R^2+z^2)^{3/2}}\]](/images/math/3/7/9/3799f1adb400e45e9801c1bd4574df04.png)
