Magnetosztatika példák - Áramkörbe kapcsolt vezetékpárra ható erő
Feladat
- Két egymással párhuzamos, elhanyagolható ellenállású, hosszú egyenes vezeték egyik végéhez
 ellenállást, másik végéhez telepet csatlakoztatunk. A hengeres vezetékek sugara
ellenállást, másik végéhez telepet csatlakoztatunk. A hengeres vezetékek sugara  , tengelyük távolsága
, tengelyük távolsága  . (
. (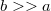 ) Mekkora
) Mekkora  ellenállásnál lesz a vezetékre ható eredő erő zérus?
ellenállásnál lesz a vezetékre ható eredő erő zérus?
Megoldás
Lássuk, milyen erők hatnak a vezetékpárra. Mivel ez egyik érben a fogyasztó felé, a másikban pedig a telep felé folyik  áram, egymásra taszító hatású Lorentz erőt fejtenek ki.
Másfelől a vezetékek egyenként ekvipotenciálisak, hiszen ideális vezetők, de az ellenálláson eső feszültség miatt a két henger eltérő potenciálon van. A párhuzamos hengerek között tehát elektromos tér is mérhető, mely szükségszerűen feltételez pozitív illetve negatív töltésfelhalmozódást a hengerek felületén. Ezen ellentétes töltések a Coulomb törvény értelmében vonzzák egymást.
Mivel mind a töltésfelhalmozódás mértéke, mind pedig a vezetékekben folyó áram nagysága függ a vezetékpárra kapcsolt
áram, egymásra taszító hatású Lorentz erőt fejtenek ki.
Másfelől a vezetékek egyenként ekvipotenciálisak, hiszen ideális vezetők, de az ellenálláson eső feszültség miatt a két henger eltérő potenciálon van. A párhuzamos hengerek között tehát elektromos tér is mérhető, mely szükségszerűen feltételez pozitív illetve negatív töltésfelhalmozódást a hengerek felületén. Ezen ellentétes töltések a Coulomb törvény értelmében vonzzák egymást.
Mivel mind a töltésfelhalmozódás mértéke, mind pedig a vezetékekben folyó áram nagysága függ a vezetékpárra kapcsolt  ellenállás mértékétől, elképzelhető, hogy az ellenállás helyes megválasztásával a Coulomb és a Lorentz erők kiolthatják egymást.
ellenállás mértékétől, elképzelhető, hogy az ellenállás helyes megválasztásával a Coulomb és a Lorentz erők kiolthatják egymást.
Kapcsoljunk  feszültséget a rendszerre. Ekkor a vezetékekben:
feszültséget a rendszerre. Ekkor a vezetékekben:
![\[I=\dfrac{U}{R}\]](/images/math/2/c/2/2c209e03d32f73c6aaf715ba26cecbaa.png)
áram folyik. A 6. feladatsor 2. feladatából tudjuk, hogy a végtelen, áramjárta vezetők tengelyüktől  távolságra:
távolságra:
![\[B=\dfrac{\mu_0 I}{2\pi r}\]](/images/math/4/9/8/49825c8d7f84ad881fbe5689cc0d5946.png)
mágneses teret keltenek. ez a tér örvényesen veszi körül a vezetéket. Ezek alapján az egyik vezeték a másik vezeték helyén:
![\[B=\dfrac{\mu_0 I}{2\pi b}\]](/images/math/b/4/8/b485b9f390234fece7049fe5ed5336b5.png)
mágneses teret indukál, melyet a második vezeték teljes keresztmetszete mentén homogénnek tekintünk. (megtehetjük, hiszen 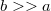 ) Ebben az erőtérben a második vezető
) Ebben az erőtérben a második vezető  hosszára ható Lorentz erő:
hosszára ható Lorentz erő:
![\[\vec{F_{Lor}}=I(\vec{l}\times \vec{B})\]](/images/math/b/5/c/b5cda4c790980e1c9620c95820628f25.png)
Belátható, hogy ennek iránya a másik vezetőtől eltaszító mutat, nagysága pedig a vektorok ortogonalitása miatt:
![\[F_{Lor}=IBl=\dfrac{\mu_0 I^2 l}{2\pi b}=\dfrac{\mu_0 U^2 l}{2\pi R^2 b}\]](/images/math/1/2/f/12fe19fb3f18bc7742f8c9c68528c0f1.png)
Nézzük most a Coulomb kölcsönhatást! A Párhuzamos hengeres vezetékek kapacitása megoldásából tudjuk, hogy két  sugarú, egymástól
sugarú, egymástól  távolságra levő párhuzamos vezető henger, melyre
távolságra levő párhuzamos vezető henger, melyre  feszültséget kapcsolunk, kondenzátorként viselkedik. Ennek értelmében az egyik henger egységnyi hosszán
feszültséget kapcsolunk, kondenzátorként viselkedik. Ennek értelmében az egyik henger egységnyi hosszán  míg a másik hengeren
míg a másik hengeren 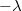 töltés jelenik meg. Az X. feladatsor X. feladatának megoldása szerint ezen párhuzamos vezetékekből összeállított kondenzátor
töltés jelenik meg. Az X. feladatsor X. feladatának megoldása szerint ezen párhuzamos vezetékekből összeállított kondenzátor  hosszán mérhető kapacitás:
hosszán mérhető kapacitás:
![\[C=\dfrac{\pi \varepsilon_0 l}{\ln \left( \dfrac{b-a}{a} \right)}\]](/images/math/b/a/e/bae686027a7860f13dc81b5eb6537dc5.png)
Ebből meghatározható a fegyverzeteken megjelenő  lineáris töltéssűrűség nagysága, ha a potenciálkülönbség
lineáris töltéssűrűség nagysága, ha a potenciálkülönbség  :
:
![\[\lambda=\dfrac{Q}{l}=\dfrac{CU}{l}=\dfrac{\pi \varepsilon_0 U}{\ln \left( \dfrac{b-a}{a} \right)}\]](/images/math/c/b/d/cbd8c51382c375f1d5d8e5dfae67cfa7.png)
Az első hengeren megjelenő  töltéssűrűség elektromos terét a Y. feladatsor Y. feladatát segítségül hívva határozhatjuk meg. Eszerint végtelen hosszú,
töltéssűrűség elektromos terét a Y. feladatsor Y. feladatát segítségül hívva határozhatjuk meg. Eszerint végtelen hosszú,  lineáris töltéssűrűséggel ellátott vonalvezető elektromos tere a vonalvezető tengelyétől sugárirányban kifelé mutat, nagysága a tengelytől mért
lineáris töltéssűrűséggel ellátott vonalvezető elektromos tere a vonalvezető tengelyétől sugárirányban kifelé mutat, nagysága a tengelytől mért  távolságtól a következőképp függ:
távolságtól a következőképp függ:
![\[E_{(r)}=\dfrac{\lambda}{2\pi\varepsilon_0 r}\]](/images/math/0/3/0/03063b3738536043ca1fcb3c92d42bf1.png)
Eszerint a jelen feladatban szereplő  töltéssűrűségű első henger a második henger helyén:
töltéssűrűségű első henger a második henger helyén:
![\[E=\dfrac{\lambda}{2\pi\varepsilon_0 b}=\dfrac{ U}{2b \ln \left( \dfrac{b-a}{a} \right)}\]](/images/math/a/9/1/a91dece08bfb2ac9619962fd5fc9b8cd.png)
teret kelt. Feltételezzük, hogy a második henger tengelyének kicsiny 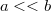 környezetén belül az első henger által keltett tér homogénnek tekinthető. Tehát a második henger
környezetén belül az első henger által keltett tér homogénnek tekinthető. Tehát a második henger  hosszúságú,
hosszúságú, 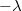 töltéssűrűségű darabjára:
töltéssűrűségű darabjára:
![\[F_{Cou}=QE=-\lambda l E=-\dfrac{\pi \varepsilon_0 lU^2}{2b\ln^2 \left( \dfrac{b-a}{a} \right)}\]](/images/math/9/2/a/92a7519fe886435cb34d5ab4c00b0394.png)
Coulomb erő hat. A feladat, hogy megtaláljuk azt az  ellenállást, melyet a vezetékpár végére kötve a Coulomb-féle vonzóerő és a Lorentz-féle taszító erő épp kioltják egymást, függetlenül attól, mekkora feszültséggel hajtjuk meg az áramkört. Az erőegyensúly feltétele:
ellenállást, melyet a vezetékpár végére kötve a Coulomb-féle vonzóerő és a Lorentz-féle taszító erő épp kioltják egymást, függetlenül attól, mekkora feszültséggel hajtjuk meg az áramkört. Az erőegyensúly feltétele:
![\[0=F_{Lor}+F_{Cou}\]](/images/math/e/c/6/ec6a6d6a5e9bf5a8b46d32bac31c4d02.png)
Behelyettesítve az erőket a megadott mennyiségekkel kifejező összefüggéseket, az alábbi egyenletet kapjuk:
![\[\dfrac{\mu_0 U^2 l}{2\pi R^2 b}=-\dfrac{\pi \varepsilon_0 lU^2}{2b\ln^2 \left( \dfrac{b-a}{a} \right)}\]](/images/math/9/5/1/9512c7f6025957693fb619e547c6a64a.png)
Az egyenletet megoldva  -re, megkapjuk a kérdéses ellenállást:
-re, megkapjuk a kérdéses ellenállást:
![\[R=\dfrac{1}{\pi}\sqrt{ \dfrac{\mu_0}{\varepsilon_0} } \ln \left( \dfrac{b-a}{a} \right) \]](/images/math/d/d/2/dd2b526116ec1a2563c1a54035b2c5f4.png)
Megjegyzés: Igen tetszetős, hogy a megoldásban megjelent az ún. vákuumimpedancia: 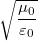 . E szép univerzális konstans csak egy dimenziótlan, pusztán geometriai paraméterektől függő faktorral van megszorozva.
. E szép univerzális konstans csak egy dimenziótlan, pusztán geometriai paraméterektől függő faktorral van megszorozva.