Magnetosztatika példák - Négyzet alakú fémkeret mágneses tere
Feladat
- Egy
 oldalú négyzet alakú fémkeretben
oldalú négyzet alakú fémkeretben  áram folyik. Határozzuk meg a mágneses térerősséget a keret középpontján átmenő, síkjára merőleges
áram folyik. Határozzuk meg a mágneses térerősséget a keret középpontján átmenő, síkjára merőleges  tengely mentén!
tengely mentén!
Megoldás
A keret által létrehozott tér a négy darab él terének összegeként írható le. A véges hosszúságú,  áram által átjárt egyenes vezetékdarab mágneses terét az Egyenes vezető mágneses tere feladatában már meghatároztuk:
áram által átjárt egyenes vezetékdarab mágneses terét az Egyenes vezető mágneses tere feladatában már meghatároztuk:
![\[B=\dfrac{\mu_0 I}{4 \pi d} (\sin(\alpha_1)-\sin(\alpha_2))\]](/images/math/8/4/2/842d4aedba7cc002900468e305d77ed4.png)
Ahol  a vizsgált pont és a vezetődarab távolsága,
a vizsgált pont és a vezetődarab távolsága, 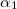 és
és 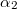 pedig a rúd két végpontjának látószöge a vizsgált pontból a vezetékhez húzott merőlegeshez képest.
A feladatban szereplő négyzetes keret középpontja felett
pedig a rúd két végpontjának látószöge a vizsgált pontból a vezetékhez húzott merőlegeshez képest.
A feladatban szereplő négyzetes keret középpontja felett  magasságban kijelölt pont egy négyzet alapú gúlává egészíti ki a rendszer geometriáját, ahogy az az ábrán látható.
ábra
magasságban kijelölt pont egy négyzet alapú gúlává egészíti ki a rendszer geometriáját, ahogy az az ábrán látható.
ábra
A gúla egy oldallapjának, mint egyenlő szárú háromszögnek a magassága megegyezik a vezető keret adott élének a vizsgált ponttól mért távolságával:
![\[d=\sqrt{z^2+\left( \dfrac{a}{2} \right)^2 }\]](/images/math/b/0/3/b037e15e95591c20002d71253a196e19.png)
A gúla élének hossza hasonló geometriai megfontolások alapján meghatározható:
![\[l=\sqrt{z^2+\left( \dfrac{a}{2} \right)^2 +\left( \dfrac{a}{2} \right)^2 }=\sqrt{z^2+ \dfrac{a^2}{2} }\]](/images/math/c/c/a/cca0158719c0b6d6c81804a1cb55ad80.png)
Ezek ismeretében meghatározható az oldallap magassága és az élek által bezárt 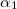 és
és 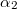 szög szinusza:
szög szinusza:
![\[\sin(\alpha_1)=\dfrac{a}{2l}=\dfrac{a}{2\sqrt{z^2+ \dfrac{a^2}{2} }}\]](/images/math/a/a/c/aac21590ea0ffc4a3249f946b3a50836.png)
![\[\sin(\alpha_2)=-\dfrac{a}{2l}=-\dfrac{a}{2\sqrt{z^2+ \dfrac{a^2}{2} }}\]](/images/math/3/1/5/315cd38a0903f803ee1e0ff2bdce2f24.png)
Már mindent ismerünk ahhoz, hogy meghatározzuk a keret egyetlen éle által a gúla csúcspontjában keltett mágneses indukció nagyságát:
![\[B=\dfrac{\mu_0 I}{4 \pi d} (\sin(\alpha_1)-\sin(\alpha_2))=\dfrac{\mu_0 I}{4 \pi \sqrt{z^2+\left( \dfrac{a}{2} \right)^2 }} \dfrac{a}{\sqrt{z^2+ \dfrac{a^2}{2} }}\]](/images/math/2/5/4/254f88084dd156d421be4530cd1f89bd.png)
A fenti 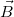 indukció vektora azonban merőleges a gúla oldallapjára, így, ha összegezni akarjuk a keret négy éle által keltett teret, akkor négy darab
indukció vektora azonban merőleges a gúla oldallapjára, így, ha összegezni akarjuk a keret négy éle által keltett teret, akkor négy darab  nagyságú, de a gúla egyes oldallapjaira merőleges vektorokat kell összegeznünk. A gúla szimmetriája miatt az egyes indukció vektorok keret síkjával párhuzamos komponensei kioltják egymást. Keret síkjára merőleges komponensei összeadódnak, így az eredő tér is a keret síkjára merőleges irányú lesz. Hogy ennek nagyságát meghatározzuk, meg kell határoznunk a fent kiszámolt
nagyságú, de a gúla egyes oldallapjaira merőleges vektorokat kell összegeznünk. A gúla szimmetriája miatt az egyes indukció vektorok keret síkjával párhuzamos komponensei kioltják egymást. Keret síkjára merőleges komponensei összeadódnak, így az eredő tér is a keret síkjára merőleges irányú lesz. Hogy ennek nagyságát meghatározzuk, meg kell határoznunk a fent kiszámolt  indukció
indukció 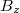 függőleges komponensét:
függőleges komponensét:
![\[B_z=B \sin(\beta)\]](/images/math/6/a/2/6a29cfa90d49597935dcc00c741b4a10.png)
Ahol  a
a 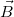 vektor keret síkjával bezárt szöge. A merőleges szárú szögek tételéből következően a gúla magassága és a gúla oldallapjának magasságvonala szintén
vektor keret síkjával bezárt szöge. A merőleges szárú szögek tételéből következően a gúla magassága és a gúla oldallapjának magasságvonala szintén  szöget zár be egymással. Tehát:
szöget zár be egymással. Tehát:
![\[\sin(\beta)=\dfrac{a}{2d}=\dfrac{a}{2\sqrt{z^2+\left( \dfrac{a}{2} \right)^2 }}\]](/images/math/6/3/7/6379323e9787fdd45b28629bac3b6015.png)
Az eredő tér így a következőnek adódik:
![\[B_e=4B_z=4B \sin(\beta)=\dfrac{\mu_0 I a^2}{2 \pi \left( z^2+\left( \dfrac{a}{2} \right)^2\right) \sqrt{z^2+ \dfrac{a^2}{2} }}\]](/images/math/3/3/7/337001ed818a1c8c53f6af83e5860232.png)