Termodinamika példák - Ideális gáz részecskéinek energia szerinti eloszlása

Feladat

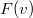1. Az $\setbox0\hbox{$F(v)$}% \message{//depth:\the\dp0//}% \box0%$ sebességeloszlási függvényből a 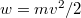$\setbox0\hbox{$w=mv^2/2$}% \message{//depth:\the\dp0//}% \box0%$ összefüggés felhasználásával vezessük le az 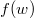$\setbox0\hbox{$f(w)$}% \message{//depth:\the\dp0//}% \box0%$ energia-eloszlási függvényt, ahol 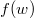$\setbox0\hbox{$f(w)$}% \message{//depth:\the\dp0//}% \box0%$ azt mutatja meg, hogy az összes molekula hányadrésze rendelkezik 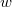$\setbox0\hbox{$w$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$w+\mathrm{d}w$}% \message{//depth:\the\dp0//}% \box0%$ 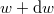közötti mozgási energiával! Mekkora a legvalószínűbb 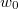$\setbox0\hbox{$w_0$}% \message{//depth:\the\dp0//}% \box0%$ energia és mennyi az átlagos kinetikus energia?

Megoldás

Az előző feladatban leírt indoklásnak megfelelően az

$\[F(v)=A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\}\]$

Maxwell-féle sebességeloszlás-függvény szigorúan véve egy valószínűségi sűrűségfüggvény. Ahhoz, hogy az energia szerinti eloszlást (matematikailag ismét csak sűrűségfüggvényt) megkapjuk, egy mértéktranszformációt kell végrehajtanunk.

Ez azt jelenti, hogy felírjuk a gázmolekulák 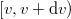$\setbox0\hbox{$[v,v+\mathrm{d}v)$}% \message{//depth:\the\dp0//}% \box0%$ sebességintervallumba eső hányadát és ezt megfeleltetjük a 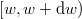$\setbox0\hbox{$[w,w+\mathrm{d}w)$}% \message{//depth:\the\dp0//}% \box0%$ energiaintervallumnak:

$\[F(v)\,\mathrm{d}v=f(w)\,\mathrm{d}w,\]$

ahol az intervallum hossza

$\[w=\frac{1}{2}\mu {v}^{2} \qquad\Leftrightarrow\qquad v=\sqrt{\frac2\mu}\sqrt{w}\]$

sebesség--energia-összefüggésből differenciálás útján kapható:

$\[ \frac{\mathrm{d}v}{\mathrm{d}w} = \sqrt{\frac2\mu} \frac1{2\sqrt{w}} \qquad\Rightarrow\qquad \mathrm{d}v=\frac{\mathrm{d}w}{\sqrt{2\mu w}}\]$

Behelyettesítés után:

$\[f\left(w\right)\mathrm{d}w=A \frac{w}{w_v} \exp\left\{ -\frac{w}{w_v} \right\} \frac{1}{\sqrt{2\mu w}}\mathrm{d}w,\]$

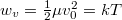ahol $\setbox0\hbox{$w_v=\frac12 \mu v_0^2=kT$}% \message{//depth:\the\dp0//}% \box0%$ a legvalószínűbb sebességhez tartozó energia.

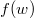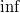Mivel $\setbox0\hbox{$f(w)$}% \message{//depth:\the\dp0//}% \box0%$ pozitív értékkészletű, $\setbox0\hbox{$0$}% \message{//depth:\the\dp0//}% \box0%$-ban és $\setbox0\hbox{$\inf$}% \message{//depth:\the\dp0//}% \box0%$-ben lecseng, azért extrémuma egyben a legvalószínűbb energia:

\[\left.\frac{\mathrm{d}f\left(w\right)}{\mathrm{d}w}\right|_{w_0}=C\exp\left\{-\frac{w_0}{kT}\right\}\left(\frac1{2\sqrt{w_0}}-\frac{\sqrt{w_0}}{kT}\right)=0\\]

\[ \frac{1}{2}-\frac{w}{kT}=0\\]

$\[ {w}_{0}={w}_{lv}=\frac{1}{2}kT\]$

Az átlagos-, várható energia:

$\stackrel{\bar }{w}={w}_{atl}}=\langle w\rangle =\underset{0}{\overset{\infty }{\int }}wf\left(w\right)\mathrm{d}w=C\underset{0}{\overset{\infty }{\int }}{w}^{\frac{3}{2}}{\mathrm{e}}^{-\frac{w}{kT}}\mathrm{d}w=C\left(-kT{w}^{\frac{3}{2}}{\mathrm{e}}^{-\frac{w}{kT}}\right)

$\[\]$

$\[ \]$

\[ 
0\end{array}-C\underset{0}{\overset{\infty }{\int }}\left(-kT\right)\frac{3}{2}\sqrt{w}{\mathrm{e}}^{-\frac{w}{kT}}\mathrm{d}w=\]

\[ 
=0-0+\frac{3}{2}kT\underset{0}{\overset{\infty }{\int }}C\sqrt{w}{\mathrm{e}}^{-\frac{w}{kT}}\mathrm{d}w=\frac{3}{2}kT\underset{0}{\overset{\infty }{\int }}f\left(w\right)\mathrm{d}w=\frac{3}{2}kT\end{array}$\]

$\[w_0=\frac12kT,\qquad \langle w\rangle=\frac32kT\]$