Termodinamika példák - Ideális gáz részecskéinek energia szerinti eloszlása
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az
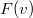sebességeloszlási függvényből a 
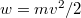összefüggés felhasználásával vezessük le az 
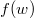energia-eloszlási függvényt, ahol 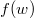azt mutatja meg, hogy az összes molekula hányadrésze rendelkezik 
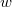és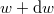 
közötti mozgási energiával! Mekkora a legvalószínűbb 
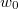energia és mennyi az átlagos kinetikus energia?
Megoldás
Az előző feladatban taglaltaknak megfelelően az
![\[F(v)=A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\}\]](/images/math/b/8/b/b8bc91fba324fff87b547f53a04ee4d0.png)
Maxwell-féle sebességeloszlás-függvény szigorúan véve egy valószínűségi sűrűségfüggvény,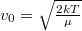 
a legvalószínűbb sebesség és 
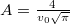állandókkal. Ahhoz, hogy az energia szerinti eloszlást (matematikailag ismét csak sűrűségfüggvényt) megkapjuk, egy mértéktranszformációt kell végrehajtanunk.
Ez fizikailag azt jelenti, hogy felírjuk a gázmolekulák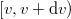 
sebességintervallumba eső hányadát és ezt megfeleltetjük a 
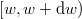energiaintervallumnak:
![\[F(v)\,\mathrm{d}v=f(w)\,\mathrm{d}w,\]](/images/math/b/1/9/b194bd8e1e25564caeee80845cdce2be.png)
ahol az intervallum kezdőpontja a
![\[w=\frac{1}{2}\mu {v}^{2} \qquad\Leftrightarrow\qquad v=\sqrt{\frac2\mu}\sqrt{w}\]](/images/math/d/a/3/da32e3bd8d64f5f73bf9da26703728d8.png)
sebesség--energia-összefüggésből, hossza pedig ebből differenciálás útján kapható:
![\[ \frac{\mathrm{d}v}{\mathrm{d}w} = \sqrt{\frac2\mu} \frac1{2\sqrt{w}} \qquad\Rightarrow\qquad \mathrm{d}v=\frac{\mathrm{d}w}{\sqrt{2\mu w}}.\]](/images/math/e/a/7/ea7cc1f34a7b21a3a571c3bfc03016b8.png)
Behelyettesítés után:
![\[f\left(w\right)\mathrm{d}w = F(v)\,\mathrm{d}v= A \frac{w}{w_v} \exp\left\{ -\frac{w}{w_v} \right\} \frac{1}{\sqrt{2\mu w}}\mathrm{d}w,\]](/images/math/3/5/4/35479a4949511b9bad2bbb4198f4824a.png)
azaz
![\[f\left(w\right) = B \sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\} ,\]](/images/math/5/f/d/5fda3318193e142b95895af3c16ee03e.png)
ahol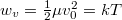 
a legvalószínűbb sebességhez tartozó energia és 
.
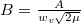Mivel 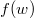pozitív értékkészletű, 
-ban és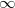 
-ben lecseng, azért extrémuma egyben a 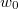-lal jelölt legvalószínűbb energia:
![\[\left.\frac{\mathrm{d}f(w)}{\mathrm{d}w}\right|_{w_0}=B\exp\left\{-\frac{w_0}{kT}\right\}\left(\frac1{2\sqrt{w_0}}-\frac{\sqrt{w_0}}{kT}\right)=0.\]](/images/math/1/7/8/178f3d39e4b96998bb4085d44debf9a2.png)
A fenti kifejezésben csak a kerek zárójelben levő rész adhat nulla értékű tényezőt, ennek a tényezőnek a megoldása a legvalószínűbb energia, ami éppen a legvalószínűbb sebességhez tartozó energiának a fele:
![\[w_0=\frac12kT=\frac12 w_v.\]](/images/math/e/a/2/ea2afb575e7070ef0b57513c177383a3.png)
Az átlagos energiát az 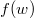függvény első momentumaként számíthatjuk:
![\[ \langle w\rangle = \int_0^\infty w f(w)\,\mathrm{d}w = B \int_0^\infty w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w.\]](/images/math/4/e/9/4e9c311b1a8efa980cc59d280899ad1d.png)
Az integrál parciális integrálással (első tényezőt deriváljuk, másodikat integráljuk) kiértékelhető alakra hozható:
![\[ \langle w\rangle = \left[-B \, kT \, w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \right]_0^\infty - \frac32(-kT) \int_0^\infty B \sqrt{w}\exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w,\]](/images/math/d/9/0/d904176aeafe8e87f62da43b19a8911a.png)
ahol az első tag a határokon eltűnik, az integrál pedig éppen a teljes energiaeloszlás-függvény integrálja, azaz egy normált sűrűségfüggvény integrálja, aminek értéke 
. Ezzel a részecskék átlagos energiája
![\[\langle w\rangle=\frac32kT\]](/images/math/9/6/9/96922c0f826d15fda9c40bde74e46a45.png)
az ekvipartíció tételével összhangban.
