Termodinamika példák - Belső energia az állapotváltozások során
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 6., 17:48-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Állapotváltozás, I. főtétel |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
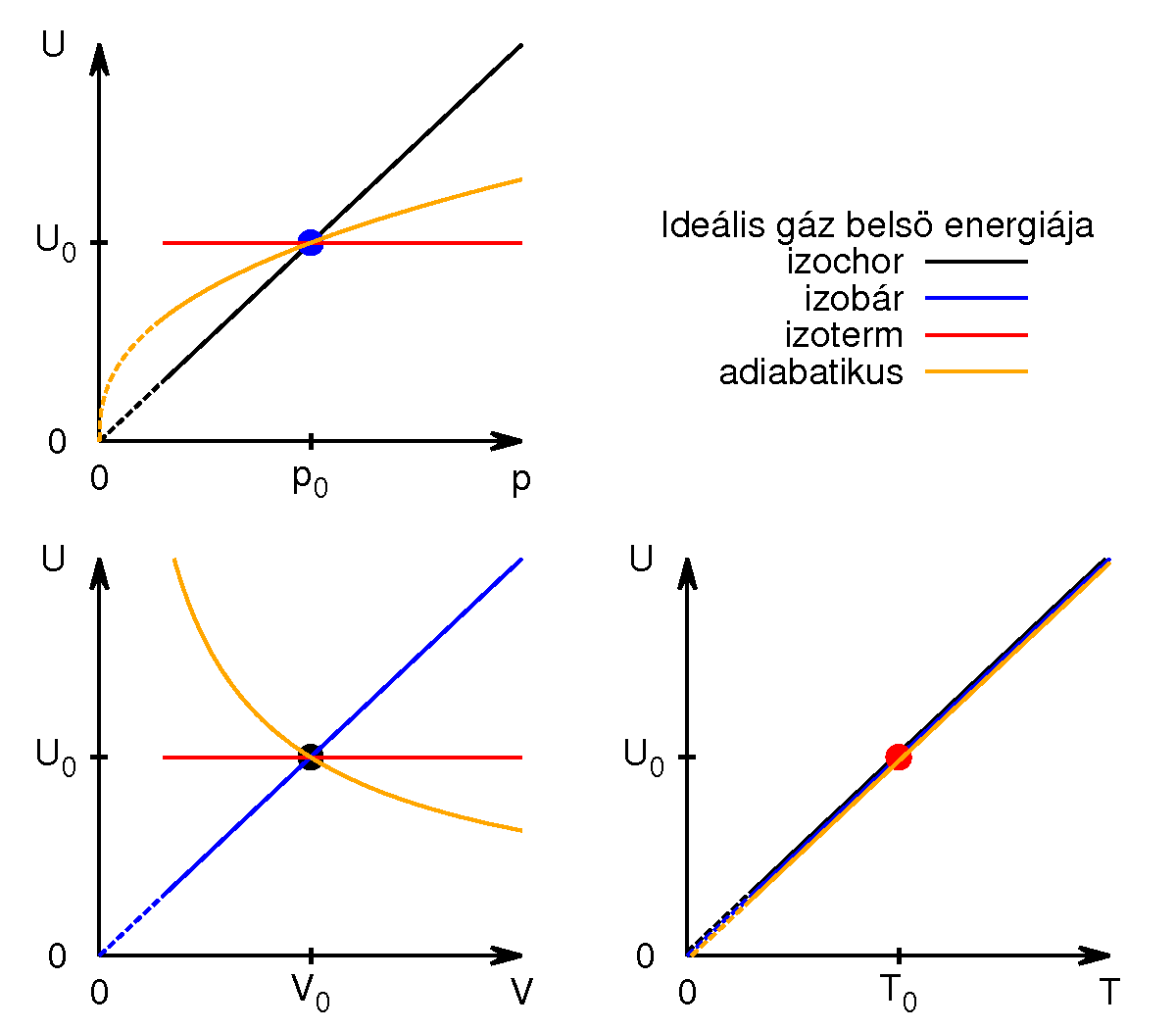
Feladat
- Ábrázolja vázlatosan ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásánál a belső energiának a hőmérséklettől-, térfogattól- és a nyomástól való függését! Legyen a belső energia az ordináta, és minden folyamatnál legyen ugyanaz a kiindulási állapot!
Megoldás
A belső energia felírásához az 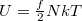 ekvipartíció tételét, a
ekvipartíció tételét, a 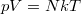 állapotegyenletet és az adiabata egyenletét használjuk.
állapotegyenletet és az adiabata egyenletét használjuk.
-
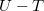 diagramon a belső energia csak a hőmérséklet függvénye, minden görbe egybeesik, az izoterm állapotváltozáshoz rögzített részecskeszám esetén egyetlen pont tartozik.
diagramon a belső energia csak a hőmérséklet függvénye, minden görbe egybeesik, az izoterm állapotváltozáshoz rögzített részecskeszám esetén egyetlen pont tartozik.
-
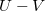 diagramon az adiabata
diagramon az adiabata 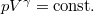 egyenletéből
egyenletéből 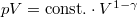 és
és 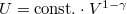 egyenletet vezethetjük le,
egyenletet vezethetjük le, 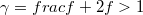 .
.
-
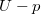 diagramon az adiabata
diagramon az adiabata 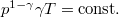 egyenletéből
egyenletéből 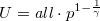 összefüggést kapjuk.
összefüggést kapjuk.
Fontos megfigyelni, melyik görbe milyen meredekséggel érkezik (elméletben) az origóba.