Termodinamika - Fázisátalakulások
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 21., 12:51-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fázisátalakulások |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Ismert mérési adatok
Mérési körülmények
| Fizikai normál állapot | Szobahőmérsékletű állapot | Kémiai standard állapot | |
| p (nyomás) | 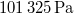
|
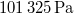
|
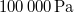
|
| T (hőmérséklet) | 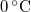 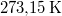
|
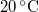 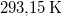
|
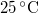 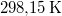
|
| VM (móltérfogat) | 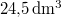
|
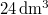
|
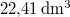
|
Anyagi tulajdonságok
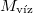 |
= | 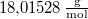 |
a víz moláris tömege |
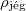 |
= | 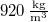 |
a jég sűrűsége 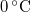 -on -on
|
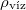 |
= | 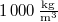 |
a víz sűrűsége 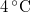 -on -on
|
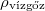 |
ideális gázként közelítjük a vízgőz sűrűségét | ||
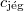 |
= | 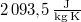 |
a jég közepes fajhője |
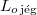 |
= | 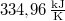 |
a jég olvadáshője |
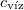 |
= | 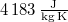 |
a víz fajhője 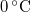 -on -on
|
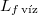 |
= | 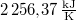 |
a víz forráshője |
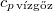 |
= | 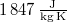 |
a vízgőz fajhője |
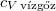 |
= | 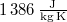 |
a vízgőz fajhője |
Feladatok
- Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő (
 ) az entalpiaváltozással (
) az entalpiaváltozással (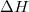 ) egyenlő!
) egyenlő!
-
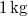 víznek normál nyomáson (
víznek normál nyomáson (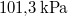 ) való elforralásához egy elektromos merülőforralón a
) való elforralásához egy elektromos merülőforralón a 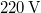 -os feszültségforrásból
-os feszültségforrásból 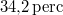 -en át
-en át 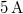 áramot kell átfolyatni. A gázállandó
áramot kell átfolyatni. A gázállandó 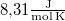 , a víz moláris tömege
, a víz moláris tömege 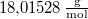 .
.
Határozzuk meg a víz- a) entalpia-,
- b) entrópia- és
- c) belső energiaváltozását ebben a folyamatban!
- Henger alakú edényben
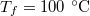 hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben
hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben 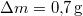 víz lecsapódik. A víz moláris tömege
víz lecsapódik. A víz moláris tömege 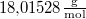 A folyamat során a nyomás a
A folyamat során a nyomás a 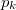 külső légnyomással egyenlő.
külső légnyomással egyenlő.
Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?
- Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának
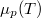 hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot
hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot 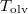 -val, a forráspontot
-val, a forráspontot 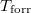 -ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!
-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!
- Felhasználva, hogy az olvadáspont az állandó nyomáson felvett
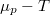 diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
- A szilárd-folyadék egyensúlyi görbének (olvadási görbe) közelítő meghatározására gyakran használják a
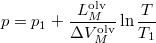 összefüggést (
összefüggést ( a
a 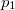 nyomáson,
nyomáson,  a
a  nyomáson érvényes olvadáspont, az egyenletben szereplő
nyomáson érvényes olvadáspont, az egyenletben szereplő 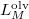 az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása),
az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), 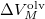 pedig a móltérfogat változása az olvadásnál).
pedig a móltérfogat változása az olvadásnál).
- a) Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!
- b) Mutassuk ki, hogy a
 -hez képest kis
-hez képest kis 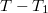 érték eseten az egyensúlyi nyomás lineárisan változik a
érték eseten az egyensúlyi nyomás lineárisan változik a 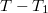 különbséggel!
különbséggel!
- A jég olvadáshője
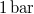 nyomáson
nyomáson 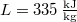 . A jég és a víz fajlagos térfogatának aránya
. A jég és a víz fajlagos térfogatának aránya 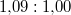 . Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
- Ha a nyomást
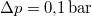 -ral megnöveljük, akkor a víz forrási hőmérséklete
-ral megnöveljük, akkor a víz forrási hőmérséklete 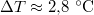 -kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!
-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!
- A szilárd argon
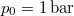 nyomáson
nyomáson 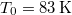 hőmérsékleten olvad meg. Olvadáshője ekkor
hőmérsékleten olvad meg. Olvadáshője ekkor 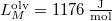 , móltérfogatának változása
, móltérfogatának változása 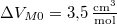 . A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a
. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a 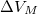 móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg
móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg 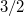 -ik hatványával arányos.
-ik hatványával arányos.
Mekkora nyomást kell alkalmaznunk ahhoz, hogy az olvadási hőmérséklet megkétszereződjék?
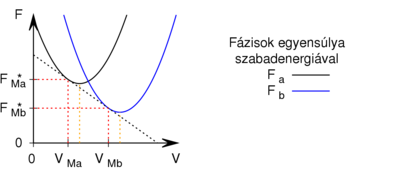
- Egy homogén anyag adott hőmérsékleten két fázisban (
 és
és  ) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
Mutassuk ki, hogy egyensúlyi állapotban a fázisok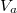 és
és 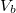 térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
- Az ábrán különböző mennyiségek hőmérsékletfüggését mutatjuk be a
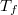 fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?
fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?

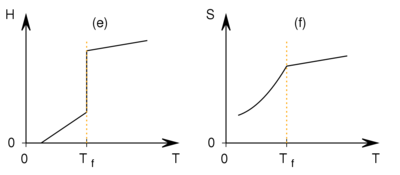

![\[\Delta H = W_\text{el} = 2{,}26\,\mathrm{MJ}\]](/images/math/4/f/d/4fdaf5770143071de6a318dd403592b3.png)
![\[\Delta S = 6{,}06\,\mathrm{\frac{kJ}{K}}\]](/images/math/7/2/7/7276d2981b6be7939e2cbb7053cfb7e9.png)
![\[\Delta U=\Delta H-\frac{m}{M}RT=2{,}09\,\mathrm{MJ}\]](/images/math/0/8/9/089fe9b22dd39aba913ca295f3f5cd56.png)
![\[\Delta W=p_k\left(V_1-V_2\right)=\frac{RT_f}{M}\Delta m=120\,\mathrm{J}\]](/images/math/0/1/c/01c0c0abb9f739cbff493a96bc03ec39.png)
![\[\left(\frac{\partial G}{\partial T}\right)_p=-S\]](/images/math/5/d/3/5d3e0ea157a966637bfd4bc7513fc8bd.png)
![\[\left(\frac{\partial \mu }{\partial p}\right)_T= V_M\]](/images/math/2/5/a/25a4030c915d37e859e677c758ddfc3f.png)
 -ekre érvényes
-ekre érvényes 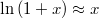 összefüggést.
összefüggést. ![\[\mathrm{d}T=-\frac{0{,}09v_\text{víz}T}{L}\,\mathrm{d}p= -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p\]](/images/math/2/b/7/2b73b88d36a28976c45ec8366c83d6ee.png)
![\[L_f\approx \frac{\Delta p}{\Delta T}\frac{RT^2}{p_kM}=2253\,\mathrm{\frac{kJ}{kg}}\]](/images/math/4/c/7/4c7c0dfc446c66a05097776d64fc920c.png)
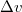 hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet!
hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet! ![\[p=p_0+\frac{2L}{3\Delta v_0}\left(1-\left(\frac{T_0}{T}\right)^{3/2}\right)=1449\,\mathrm{bar}\]](/images/math/b/5/9/b59affbd1e174e38c0177e77ed696768.png)
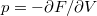 , ill.
, ill. 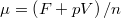 ), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!
), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!