Termodinamika példák - Gázcsere tartályok közt
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Két azonos térfogatú tartály kacsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben
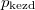 nyomású hidrogéngáz, a másikban kétszer akkora nyomású hidrogéngáz van. A gázok
nyomású hidrogéngáz, a másikban kétszer akkora nyomású hidrogéngáz van. A gázok  hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos
hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos 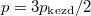 egyensúlyi nyomás alakul ki!
egyensúlyi nyomás alakul ki!
Megoldás
Amikor a gázcsere kis lyukon keresztül valósul meg a tartályok között, feltehetjük, hogy a gáz egy-egy tartályon belül végig egyensúlyi állapotban marad. Ha a lyuk mérete sokkal kisebb az átlagos szabad úthossznál, akkor a rajta keresztül időegység alatt távozó molekulák száma megegyezik azzal, amit a gáz kinetikus elméletében a nyomás tárgyalásakor a tartály falának ugyanakkora felületét időegység alatt érő molekulák számára kapunk (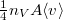 ). A molekulák száma az egyes tartályokban időben változik, ezt általánosan differenciálegyenlet-rendszerrel írhatjuk le:
). A molekulák száma az egyes tartályokban időben változik, ezt általánosan differenciálegyenlet-rendszerrel írhatjuk le:
![\[ \frac{\mathrm{d}N^{(1)}}{\mathrm{d}t} = - \frac14 n_V^{(1)}\langle v \rangle A + \frac14 n_V^{(2)}\langle v \rangle A,\]](/images/math/b/3/4/b347c9f105aeb903ab882413b764b9f2.png)
ahol az egyes tartályokat zárójelbe tett számmal indexeltük, de a molekulák átlagos sebessége a két tartályban az azonos 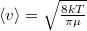 , hiszen a két tartály hőmérséklete és töltőanyaga is azonos.
, hiszen a két tartály hőmérséklete és töltőanyaga is azonos.
Az anyagmegmaradás értelmében a második tartályban levő molekulák száma 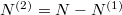 , aminek értelmében
, aminek értelmében 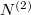 megváltozása is kifejezhető az előző mennyiségekkel:
megváltozása is kifejezhető az előző mennyiségekkel:
![\[ \frac{\mathrm{d}N^{(1)}}{\mathrm{d}t} = -\frac{\mathrm{d}N^{(2)}}{\mathrm{d}t}. \]](/images/math/1/6/c/16c0565dd0bb4bb61f994f9bde059e3a.png)
Felhasználva ezt és 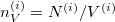 definíciót, ismét szétválasztható differenciálegyenletet kapunk:
definíciót, ismét szétválasztható differenciálegyenletet kapunk:
![\[ V^{(1)} \frac{\mathrm{d}n_V^{(1)}}{\mathrm{d}t} = - \frac14 \langle v \rangle A \left(1+\frac{V^{(1)}}{V^{(2)}}\right)n_V^{(1)} + \frac14 \langle v \rangle A \frac{N}{V^{(2)}}\]](/images/math/c/5/3/c536320e705e8112efb5a2d6d888630d.png)
Egyensúly esetén 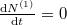 , azaz
, azaz 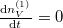 :
:
![\[ \left(1+\frac{V^{(1)}}{V^{(2)}}\right)n_V^{(1)} = \frac{N}{V^{(2)}},\]](/images/math/1/f/8/1f8281c1229069750412e3a2306414bb.png)
amiből
![\[ n_V^{(1)} = \frac{N}{V^{(1)}+V^{(2)}}. \]](/images/math/7/2/f/72f2d7f499939089b0f5e61f19eea65d.png)
Analóg módon kapjuk, hogy egyensúlyban 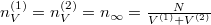 , azaz a két tartályban megegyezik a gáz sűrűsége, a feladatkiírás szerint hőmérséklete is, így nyomása
, azaz a két tartályban megegyezik a gáz sűrűsége, a feladatkiírás szerint hőmérséklete is, így nyomása
![\[ p = \frac{N^{(1)}+N^{(2)}}{V^{(1)}+V^{(2)}} kT = \frac{N}{V^{(1)}+V^{(2)}} kT. \]](/images/math/6/8/8/688250f6731d07fd8be439c1bc444151.png)
Speciálisan a feladat szerint 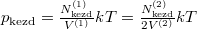 és
és 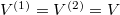 , azaz
, azaz 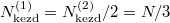 , ezeket összevetve a kialakuló egyensúlyi nyomás
, ezeket összevetve a kialakuló egyensúlyi nyomás 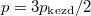 .
.
Kiegészítés
A felírt
![\[ \frac{\mathrm{d}n_V^{(1)}}{\mathrm{d}t} = - \alpha n_V^{(1)} + \beta,\]](/images/math/b/b/6/bb65eed8abab11ad07fc70a62c5cd3c4.png)
![\[ \alpha = \frac14 \langle v \rangle A \left(\frac{V^{(1)}+V^{(2)}}{V^{(1)} V^{(2)}}\right), \qquad \beta = \frac14 \langle v \rangle A \frac{N}V^{(1)} {V^{(2)}} = n_\infty \alpha \]](/images/math/7/6/9/7692050dfcf66eb15a73fcc0782082c1.png)
differenciálegyenlet megoldása
![\[ \frac{\mathrm{d}n_V^{(1)}}{\mathrm{d}t} = \frac{\mathrm{d}(n_V^{(1)}-n_\infty)}{\mathrm{d}t} - \alpha n_V^{(1)} + \alpha (n_V^{(1)}-n_\infty)\]](/images/math/d/c/2/dc28da4a04871741505c829be05480cd.png)
felírásban már triviális:
![\[ n_V^{(1)}-n_\infty = c \, e^{ -\alpha t }, \]](/images/math/1/1/e/11e7d1c5af215810b4f018a37896ffb3.png)
és kezdeti feltételre illesztése 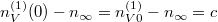 .
Az első tartályban levő részecskék száma exponenciálisan lecsengve közelít az egyensúlyi
.
Az első tartályban levő részecskék száma exponenciálisan lecsengve közelít az egyensúlyi 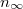 értékhez:
értékhez:
![\[ n_V^{(1)} = n_\infty + (n_{V0}^{(1)}-n_\infty) e^{ -\alpha t }. \]](/images/math/f/7/1/f717624f4e44c3652415635010fabbb0.png)
Diszkusszió
Ha 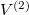 térfogatot végtelennek tekintjük, akkor a gáz szökésének speciális esetét kapjuk:
térfogatot végtelennek tekintjük, akkor a gáz szökésének speciális esetét kapjuk: 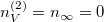 :
:
![\[ n_V^{(1)} = n_{V0}^{(1)} e^{ -\alpha t }. \]](/images/math/6/5/c/65c2eb196039185ce887b3af4d7cebb8.png)