Termodinamika példák - Van der Waals-gáz egyensúlyi hőmérséklete

Feladat

1. Van der Waals-gáz belső energiájának térfogatfüggése az alábbi összefüggéssel adható meg:
   $\[ U = c_V mT - \frac{m^2}{M^2}\frac{a}{V},\]$
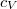   ahol $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ a gáz tömege, $\setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0%$ a móltömeg, $\setbox0\hbox{$c_V$}% \message{//depth:\the\dp0//}% \box0%$ az állandó térfogaton mért fajhő, $\setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0%$ állandó.
   Egy hőszigetelt tartályt rögzített, jó hővezető anyagból készített fal választ két részre, amelyekbe azonos tömegű Van der Waals-gázt vezettünk be. A kezdeti állapotjellemzők: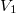 $\setbox0\hbox{$V_1$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$T_1$}% \message{//depth:\the\dp0//}% \box0%$, illetve $\setbox0\hbox{$V_2$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$T_2$}% \message{//depth:\the\dp0//}% \box0%$.
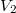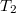   • a) Mennyi lesz a végső egyensúlyi hőmérséklet?
   • b) Hogyan módosul a válasz, ha a gáz betöltése után az elválasztó falat rögtön kivesszük?

Megoldás

Az egész tartályt tekintve az összes 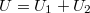$\setbox0\hbox{$U=U_1+U_2$}% \message{//depth:\the\dp0//}% \box0%$ belső energia állandó.

a) A hővezető fal megőrzi az egyes rekeszek térfogatát, de megengedi köztük a hőcserét, így a közös hőmérséklet kialakulását:

$\[ c_V m T_1-\frac{m^2}{M^2}\frac{a}{V_1} + c_V m T_2-\frac{m^2}{M^2} \frac{a}{V_2} = c_V m T-\frac{m^2}{M^2}\frac{a}{V_1} + c_V m T-\frac{m^2}{M^2} \frac{a}{V_2}. \]$

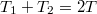Ebből egyszerűsítések után $\setbox0\hbox{$T_1+T_2=2T$}% \message{//depth:\the\dp0//}% \box0%$, azaz a közös hőmérséklet

$\[ T=\frac{T_1+T_2}{2}. \]$

b) Ha kivesszük a válaszfalat, a gáz sűrűsége mindkét rekeszben azonos lesz, a végállapotban a 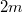$\setbox0\hbox{$2m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű gáz a 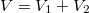$\setbox0\hbox{$V=V_1+V_2$}% \message{//depth:\the\dp0//}% \box0%$ térfogatot tölti ki:

$\[ c_V m T_1-\frac{m^2}{M^2}\frac{a}{V_1} + c_V m T_2-\frac{m^2}{M^2} \frac{a}{V_2} = c_V 2m T-\frac{(2m)^2}{M^2}\frac{a}{V_1+ V_2}.\]$

Egyszerűsítések

$\[ T_1+ T_2-\frac{ma}{c_V M^2}\left(\frac 1{V_1}+\frac 1{V_2}\right) = 2T-\frac{ma}{c_V M^2}\left(\frac 4{V_1+ V_2}\right), \]$

és közös nevezőre hozás után a közös hőmérséklet

$\[ T=\frac{T_1+ T_2} 2-\frac{ma}{2 c_V M^2}\cdot \frac{{\left( V_2- V_1\right)}^2}{\left( V_1+ V_2\right) V_1 V_2}. \]$