Termodinamika példák - Szilárd testek közelítő állapotegyenlete mérhető mennyiségekből
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 29., 11:07-kor történt szerkesztése után volt.
Feladat
- Szilárd testek hőtágulási együtthatója, illetve izotermikus kompresszibilitása alacsony hőmérsékleten az alábbi összefüggésekkel adható meg: (
![\[ \beta_p = \frac{3aT^3}{V},\qquad \kappa_T=\frac{b}{V} \]](/images/math/c/4/5/c452cee6e528e707dc57f0f8a8cb00da.png)
 és
és  állandók). Határozzuk meg a szilárd test ilyenkor érvényes állapotegyenletét!
állandók). Határozzuk meg a szilárd test ilyenkor érvényes állapotegyenletét!
Megoldás
Tekintve az izobár hőtágulási együttható definícióját
![\[ \beta_p = \frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_p = \frac{3aT^3}{V} \]](/images/math/0/8/2/082c6a7c8567762caa3965d2771d66b0.png)
összefüggést kapjuk, amit integrálva
![\[ V\left(p,T\right) = \frac34 a T^4+f\left(p\right). \]](/images/math/3/5/0/350abcb7b1c31a8581645249e514993a.png)
Vessük össze az izoterm kompresszibilitás definícióját az előbb kapott, ismeretlen függvényt tartalmazó állapotegyenlettel:
![\[ \kappa_T = -\frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_T = -\frac{1}{V} \frac{\mathrm{d}f(p)}{\mathrm{d}p} = \frac{b}{V}, \]](/images/math/0/3/1/031ebd489d147d6e9a90824fbccef1f5.png)
az 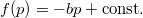 összefüggést kapjuk, amivel az állapotegyenlet:
összefüggést kapjuk, amivel az állapotegyenlet:
![\[ V\left(p,T\right) = \frac34 a T^4 - bp + \mathrm{const.} \]](/images/math/7/1/2/7127c8dd2c9b371a30411582c95b6c67.png)