Ismert összefüggések
Két fázis egyensúlya esetén érvényes
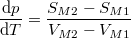 |
a Clausius–Clapeyron-egyenlet és
|
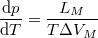 |
a Clapeyron-egyenlet,
|
ahol 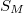 ,
, 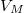 és
és 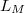 rendre a moláris entrópia, térfogat és átalakulási hő.
rendre a moláris entrópia, térfogat és átalakulási hő.
Levezetésük a Szilárd-folyadék egyensúlyi görbéről szóló feladatban található.
Ismert mérési adatok
Mérési körülmények
Anyagi tulajdonságok
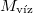 |
= |
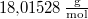 |
a víz moláris tömege
|
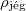 |
= |
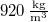 |
a jég sűrűsége 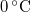 -on -on
|
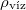 |
= |
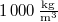 |
a víz sűrűsége 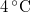 -on -on
|
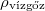 |
|
ideális gázként közelítjük a vízgőz sűrűségét
|
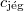 |
= |
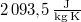 |
a jég közepes fajhője
|
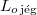 |
= |
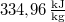 |
a jég olvadáshője
|
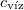 |
= |
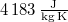 |
a víz fajhője 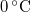 -on -on
|
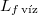 |
= |
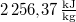 |
a víz forráshője
|
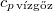 |
= |
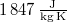 |
a vízgőz fajhője
|
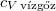 |
= |
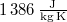 |
a vízgőz fajhője
|
Feladatok
- Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő (
 ) az entalpiaváltozással (
) az entalpiaváltozással (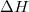 ) egyenlő!
) egyenlő!Használjuk az entalpia definícióját és az első főtételt!
-
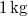 víznek normál nyomáson (
víznek normál nyomáson (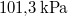 ) való elforralásához egy elektromos merülőforralón a
) való elforralásához egy elektromos merülőforralón a 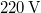 -os feszültségforrásból
-os feszültségforrásból 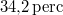 -en át
-en át 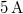 áramot kell átfolyatni. A gázállandó
áramot kell átfolyatni. A gázállandó 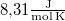 , a víz moláris tömege
, a víz moláris tömege 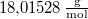 .
.
Határozzuk meg a víz
- a) entalpia-,
használjuk fel az
előző feladat eredményét az izobár átalakulási hőre.
- b) entrópia- és
használjuk az entrópia definícióját
- c) belső energiaváltozását ebben a folyamatban!
írjuk fel az entalpiaváltozás és belső energiaváltozás összefüggését, hanyagoljuk el a víz térfogatát a gőzéhez képest, és a gőzt tekintsük ideális gáznak.
- Henger alakú edényben
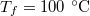 hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben
hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben 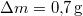 víz lecsapódik. A víz moláris tömege
víz lecsapódik. A víz moláris tömege 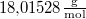 A folyamat során a nyomás a
A folyamat során a nyomás a 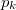 külső légnyomással egyenlő.
külső légnyomással egyenlő.
Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?
- Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának
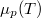 hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot
hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot 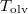 -val, a forráspontot
-val, a forráspontot 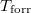 -ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!
-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!Használjuk fel a
egyenletet, a kémiai potenciál és a szabad entalpia összefüggését, továbbá két fázis egyensúlyának feltételét.
- Felhasználva, hogy az olvadáspont az állandó nyomáson felvett
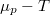 diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?A nyomásváltozás a
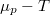
görbét eltolja, mégpedig a két fázisban általában különbözőképpen. A görbe eltolódásának mértékét adott hőmérsékleten, adott fázisban a
összefüggés adja meg.
- A szilárd-folyadék egyensúlyi görbének (olvadási görbe) közelítő meghatározására gyakran használják a
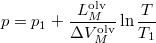 összefüggést (
összefüggést ( a
a 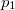 nyomáson,
nyomáson,  a
a  nyomáson érvényes olvadáspont, az egyenletben szereplő
nyomáson érvényes olvadáspont, az egyenletben szereplő 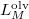 az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása),
az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), 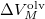 pedig a móltérfogat változása az olvadásnál).
pedig a móltérfogat változása az olvadásnál).
- a) Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!
Integráljuk a Clausius-Clapeyron-egyenletet!
- b) Mutassuk ki, hogy a
 -hez képest kis
-hez képest kis 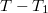 érték eseten az egyensúlyi nyomás lineárisan változik a
érték eseten az egyensúlyi nyomás lineárisan változik a 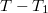 különbséggel!
különbséggel!Használjuk fel a kis

-ekre érvényes
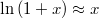
összefüggést.
- A jég olvadáshője
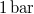 nyomáson
nyomáson 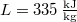 . A jég és a víz fajlagos térfogatának aránya
. A jég és a víz fajlagos térfogatának aránya 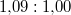 . Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
- Ha a nyomást
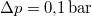 -ral megnöveljük, akkor a víz forrási hőmérséklete
-ral megnöveljük, akkor a víz forrási hőmérséklete 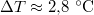 -kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!
-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!A vízgőzre alkalmazzuk az ideális gáz egyenletét, és hanyagoljuk el a víz fajlagos térfogatát a gőzéhez képest!
- A szilárd argon
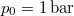 nyomáson
nyomáson 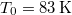 hőmérsékleten olvad meg. Olvadáshője ekkor
hőmérsékleten olvad meg. Olvadáshője ekkor 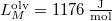 , móltérfogatának változása
, móltérfogatának változása 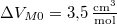 . A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a
. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a 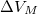 móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg
móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg 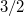 -ik hatványával arányos.
-ik hatványával arányos.
Mekkora nyomást kell alkalmaznunk ahhoz, hogy az olvadási hőmérséklet megkétszereződjék?A
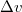
hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet!
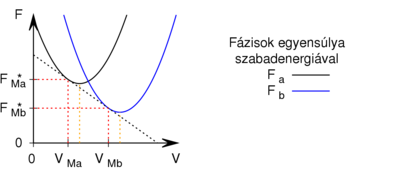
- Egy homogén anyag adott hőmérsékleten két fázisban (
 és
és  ) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
Mutassuk ki, hogy egyensúlyi állapotban a fázisok 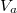 és
és 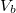 térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!fejezzük ki a nyomást és a kémiai potenciált a szabad energiával (
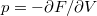
, ill.
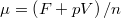
), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!
- Az ábrán különböző mennyiségek hőmérsékletfüggését mutatjuk be a
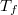 fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?
fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?


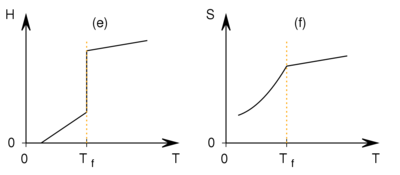

Elsőrendűek: a), b), e), h).
Másodrendűek: c)', d)', f), g).
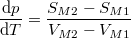
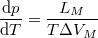
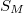 ,
, 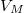 és
és 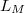 rendre a moláris entrópia, térfogat és átalakulási hő.
rendre a moláris entrópia, térfogat és átalakulási hő.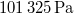
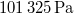
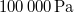
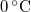
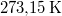
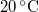
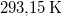
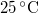
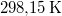
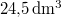
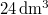
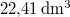
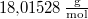
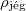
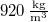
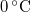 -on
-on
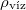
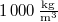
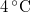 -on
-on
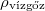
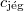
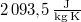
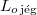
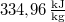
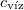
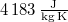
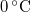 -on
-on
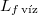
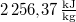
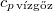
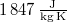
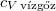
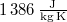
 ) az entalpiaváltozással (
) az entalpiaváltozással (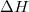 ) egyenlő!
) egyenlő! 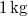 víznek normál nyomáson (
víznek normál nyomáson (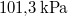 ) való elforralásához egy elektromos merülőforralón a
) való elforralásához egy elektromos merülőforralón a 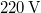 -os feszültségforrásból
-os feszültségforrásból 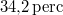 -en át
-en át 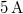 áramot kell átfolyatni. A gázállandó
áramot kell átfolyatni. A gázállandó 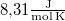 , a víz moláris tömege
, a víz moláris tömege 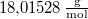 .
.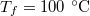 hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben
hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben 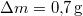 víz lecsapódik. A víz moláris tömege
víz lecsapódik. A víz moláris tömege 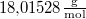 A folyamat során a nyomás a
A folyamat során a nyomás a 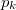 külső légnyomással egyenlő.
külső légnyomással egyenlő.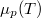 hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot
hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot 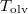 -val, a forráspontot
-val, a forráspontot 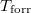 -ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!
-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől! 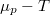 diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?
diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor? 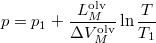 összefüggést (
összefüggést ( a
a 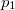 nyomáson,
nyomáson,  a
a  nyomáson érvényes olvadáspont, az egyenletben szereplő
nyomáson érvényes olvadáspont, az egyenletben szereplő 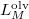 az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása),
az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), 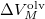 pedig a móltérfogat változása az olvadásnál).
pedig a móltérfogat változása az olvadásnál).
 -hez képest kis
-hez képest kis 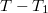 érték eseten az egyensúlyi nyomás lineárisan változik a
érték eseten az egyensúlyi nyomás lineárisan változik a 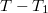 különbséggel!
különbséggel!  nyomáson
nyomáson 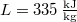 . A jég és a víz fajlagos térfogatának aránya
. A jég és a víz fajlagos térfogatának aránya 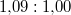 . Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!
. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!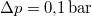 -ral megnöveljük, akkor a víz forrási hőmérséklete
-ral megnöveljük, akkor a víz forrási hőmérséklete 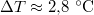 -kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!
-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét! 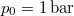 nyomáson
nyomáson 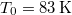 hőmérsékleten olvad meg. Olvadáshője ekkor
hőmérsékleten olvad meg. Olvadáshője ekkor 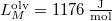 , móltérfogatának változása
, móltérfogatának változása 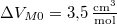 . A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a
. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a 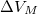 móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg
móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg 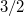 -ik hatványával arányos.
-ik hatványával arányos. és
és  ) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.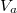 és
és 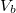 térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense! 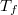 fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?
fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?

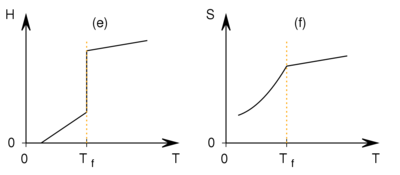

![\[\Delta H = W_\text{el} = 2{,}26\,\mathrm{MJ}\]](/images/math/4/f/d/4fdaf5770143071de6a318dd403592b3.png)
![\[\Delta S = 6{,}06\,\mathrm{\frac{kJ}{K}}\]](/images/math/7/2/7/7276d2981b6be7939e2cbb7053cfb7e9.png)
![\[\Delta U=\Delta H-\frac{m}{M}RT=2{,}09\,\mathrm{MJ}\]](/images/math/0/8/9/089fe9b22dd39aba913ca295f3f5cd56.png)
![\[\Delta W=p_k\left(V_1-V_2\right)=\frac{RT_f}{M}\Delta m=120\,\mathrm{J}\]](/images/math/0/1/c/01c0c0abb9f739cbff493a96bc03ec39.png)
![\[\left(\frac{\partial G}{\partial T}\right)_p=-S\]](/images/math/5/d/3/5d3e0ea157a966637bfd4bc7513fc8bd.png)
![\[\left(\frac{\partial \mu }{\partial p}\right)_T= V_M\]](/images/math/2/5/a/25a4030c915d37e859e677c758ddfc3f.png)
 -ekre érvényes
-ekre érvényes 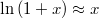 összefüggést.
összefüggést. ![\[\mathrm{d}T=-\frac{0{,}09v_\text{víz}T}{L}\,\mathrm{d}p= -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p\]](/images/math/2/b/7/2b73b88d36a28976c45ec8366c83d6ee.png)
![\[L_f\approx \frac{\Delta p}{\Delta T}\frac{RT^2}{p_kM}=2253\,\mathrm{\frac{kJ}{kg}}\]](/images/math/4/c/7/4c7c0dfc446c66a05097776d64fc920c.png)
 hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet!
hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet! ![\[p=p_0+\frac{2L}{3\Delta v_0}\left(1-\left(\frac{T_0}{T}\right)^{3/2}\right)=1449\,\mathrm{bar}\]](/images/math/b/5/9/b59affbd1e174e38c0177e77ed696768.png)
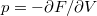 , ill.
, ill. 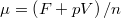 ), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!
), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!