„Termodinamika - Kinetikus gázelmélet, transzportfolyamatok” változatai közötti eltérés
A Fizipedia wikiből
a (→Ismert összefüggések: elgépelés javítása) |
|||
| (egy szerkesztő 24 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| + | <noinclude> | ||
[[Kategória:Kísérleti fizika 3. gyakorlat]] | [[Kategória:Kísérleti fizika 3. gyakorlat]] | ||
[[Kategória:Szerkesztő:Stippinger]] | [[Kategória:Szerkesztő:Stippinger]] | ||
| − | |||
| − | |||
| − | |||
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika 3. gyakorlat | | tárgynév = Kísérleti fizika 3. gyakorlat | ||
| gyaksorszám = 1 | | gyaksorszám = 1 | ||
| − | | témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok|Kinetikus gázelmélet, | + | | témakör = Termodinamika - Kinetikus gázelmélet, transzportfolyamatok |
| − | | | + | | rövid = Kinetikus gázelmélet, transzport |
| + | | fejezetlap = true | ||
}} | }} | ||
| + | == Ismert fizikai állandók == | ||
| + | <wlatex>$$ R = N_A \cdot k = 6,02 \cdot 10^{23}\ \mathrm{mol^{-1}} \cdot 1,381 \cdot 10^{-23}\ \mathrm{J \cdot K^{-1}} = 8,314\ \mathrm{J \cdot mol^{-1} \cdot K^{-1}} $$ | ||
| + | ahol $R$ az egyetemes gázálladó, $k$ a ''Boltzmann''-állandó, $N_A$ az ''Avogadro''-szám.</wlatex> | ||
| + | == Ismert összefüggések == | ||
| + | <wlatex>'''Az ideális gáz állapotegyenlete''' | ||
| + | $$ pV = NkT \equiv nRT, $$ | ||
| + | ahol $p$ a gáz nyomása, $V$ a térfogata, $T$ pedig a hőmérséklete. | ||
| − | + | '''A ''Maxwell''-féle sebességeloszlás''' | |
| + | $$F(v)=A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\}$$ | ||
| + | alakú valószínűségi sűrűségfüggvény, ahol $v_0$ a legvalószínűbb sebesség és $A=\frac{4}{v_0\sqrt{\pi}}$ a normáló tényező. | ||
| + | Az eloszlásra jellemző sebességek kifejezhetőek a $T$ hőmérséklettel és a $\mu$ a molekulatömeggel: | ||
| + | {| style="margin-left: auto; margin-right: auto;" | ||
| + | | rowspan="3" style="min-width: 250px; text-align: center;" | [[Fájl:Maxwell-sebességeloszlás sémája.svg|200px]] | ||
| + | | align="right" | $v_0$ || = || $\displaystyle \sqrt{\frac{2kT}{\mu}}$ || legvalószínűbb sebesség, | ||
| + | |- | ||
| + | | align="right" | $\langle v \rangle$ || = || $\displaystyle \sqrt{\frac{8kT}{\pi\mu}}$ || sebesség nagyságának átlaga, | ||
| + | |- | ||
| + | | align="right" | $\sqrt{\langle v^2 \rangle}$ || = || $\displaystyle \sqrt{\frac{3kT}{\mu}}$ || sebességnégyzet átlagának gyöke. | ||
| + | |} | ||
| − | + | '''A kinetikus gázelmélet néhány eredménye''' | |
| − | + | {| style="margin-left: auto; margin-right: auto;" | |
| − | + | | align="right" | $\langle l \rangle$ || = || $\displaystyle \frac{1}{\sqrt{2}\, n_V \sigma}$ || a gázrészecskék átlagos szabad úthossza, | |
| − | + | |- | |
| − | + | | align="right" | $\dot N$ || = || $\displaystyle \frac14 n_V A \langle v \rangle $ || az $A$ nagyságú felületetnek egyensúlyban <br /> időegység alatt nekiütköző részecskék száma, | |
| − | + | |- | |
| − | + | | align="right" | $D$ || = || $\displaystyle \frac13 \langle l \rangle \langle v \rangle$ || a gáz diffúzióállandója, | |
| − | + | |- | |
| − | + | | align="right" | $\eta$ || = || $\displaystyle -\frac13 \langle l \rangle \langle v \rangle n_V \mu $ || a gáz viszkozitása, | |
| − | + | |} | |
| − | + | ahol $\sigma$ a gázrészecskék ütközési hatáskeresztmetszete, $n_V$ a gáz részecskeszám-sűrűsége, $\mu$ a részecskék tömege, $\langle v \rangle$ pedig a részecskék sebessége nagyságának átlaga. | |
| − | + | ||
| − | + | Egy $A$ nagyságú keresztmetszeten átadott hőteljesítmény | |
| − | + | {| style="margin-left: auto; margin-right: auto;" | |
| − | + | | align="right" | $\dot Q$ || = || $\displaystyle -\lambda A \frac{\mathrm{d}T}{\mathrm{d}z}$ || folytonos hőmérsékletprofil esetén, | |
| − | + | |- | |
| + | | align="right" | $\dot Q$ || = || $\displaystyle A\alpha \left(T_1-T_0\right)$ || érintkezésbe hozott felületek esetén, | ||
| + | |} | ||
| + | ahol $\lambda$ a hővezetési együttható, $\alpha$ a hőátadási tényező, $T$ pedig a helyfüggő hőmérséklet. | ||
| + | </wlatex> | ||
| + | |||
| + | == Feladatok == | ||
| + | </noinclude> | ||
| + | {{:Termodinamika példák - Egyatomos ideális gáz nyomása belső energiával}}{{Megoldás|link=Termodinamika példák - Egyatomos ideális gáz nyomása belső energiával}} | ||
| + | {{:Termodinamika példák - Stern-kísérlet}}{{Megoldás|link=Termodinamika példák - Stern-kísérlet}} | ||
| + | {{:Termodinamika példák - Ideális gáz részecskéinek energia szerinti eloszlása}}{{Megoldás|link=Termodinamika példák - Ideális gáz részecskéinek energia szerinti eloszlása}} | ||
| + | {{:Termodinamika példák - Vákuum}}{{Megoldás|link=Termodinamika példák - Vákuum}} | ||
| + | {{:Termodinamika példák - Diffúzió és belső súrlódás}}{{Megoldás|link=Termodinamika példák - Diffúzió és belső súrlódás}} | ||
| + | {{:Termodinamika példák - Gáz szökése}}{{Megoldás|link=Termodinamika példák - Gáz szökése}} | ||
| + | {{:Termodinamika példák - Gázcsere tartályok közt}}{{Megoldás|link=Termodinamika példák - Gázcsere tartályok közt}} | ||
| + | {{:Termodinamika példák - Gázcsere két gázzal}}{{Megoldás|link=Termodinamika példák - Gázcsere két gázzal}} | ||
| + | {{:Termodinamika példák - Lineáris hőmérsékletprofil}}{{Megoldás|link=Termodinamika példák - Lineáris hőmérsékletprofil}} | ||
| + | {{:Termodinamika példák - Jég fagyása}}{{Megoldás|link=Termodinamika példák - Jég fagyása}} | ||
| + | {{:Termodinamika példák - Hővezetés}}{{Megoldás|link=Termodinamika példák - Hővezetés}} | ||
A lap jelenlegi, 2015. május 19., 22:07-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
Gyakorlatok listája:
|
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Ismert fizikai állandók
![\[ R = N_A \cdot k = 6,02 \cdot 10^{23}\ \mathrm{mol^{-1}} \cdot 1,381 \cdot 10^{-23}\ \mathrm{J \cdot K^{-1}} = 8,314\ \mathrm{J \cdot mol^{-1} \cdot K^{-1}} \]](/images/math/8/0/4/80417d968d780e11850deb51e0928145.png)
ahol 
az egyetemes gázálladó, 
a Boltzmann-állandó,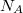 
az Avogadro-szám.
Ismert összefüggések
Az ideális gáz állapotegyenlete
![\[ pV = NkT \equiv nRT, \]](/images/math/b/c/3/bc37f5be08d6e2cfc79eff45add6e3e2.png)
ahol 
a gáz nyomása, 
a térfogata, 
pedig a hőmérséklete.
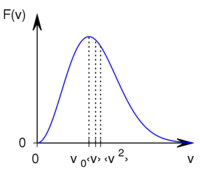
A Maxwell-féle sebességeloszlás
![\[F(v)=A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\}\]](/images/math/b/8/b/b8bc91fba324fff87b547f53a04ee4d0.png)
alakú valószínűségi sűrűségfüggvény, ahol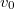 
a legvalószínűbb sebesség és 
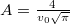a normáló tényező.
Az eloszlásra jellemző sebességek kifejezhetőek a hőmérséklettel és a 
a molekulatömeggel:
|
|
= |  |
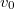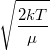legvalószínűbb sebesség, |
 |
= |  |
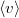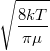sebesség nagyságának átlaga, | |
 |
= |  |
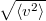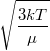sebességnégyzet átlagának gyöke. |
A kinetikus gázelmélet néhány eredménye
 |
= |  |
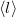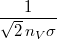a gázrészecskék átlagos szabad úthossza, |
 |
= |  |
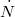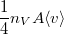az  nagyságú felületetnek egyensúlyban időegység alatt nekiütköző részecskék száma, |
 |
= |  |
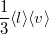a gáz diffúzióállandója, |
 |
= |  |
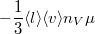a gáz viszkozitása, |
ahol 
a gázrészecskék ütközési hatáskeresztmetszete,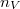 
a gáz részecskeszám-sűrűsége, a részecskék tömege, 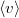pedig a részecskék sebessége nagyságának átlaga.
Egy nagyságú keresztmetszeten átadott hőteljesítmény
 |
= |  |
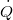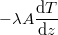folytonos hőmérsékletprofil esetén, |
| |
= |  |
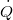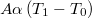érintkezésbe hozott felületek esetén, |
ahol 
a hővezetési együttható, 
a hőátadási tényező, pedig a helyfüggő hőmérséklet.
Feladatok
- Fejezze ki az egyatomos ideális gáz nyomását a gáz
belső energiájával és térfogatával!Végeredmény![\[p=\frac{2U}{3V}\]](/images/math/7/9/a/79a5ef5aee3e9a6d7f09326b91f3a4b4.png)
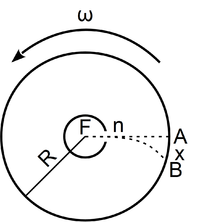
- Stern híres kísérletében, amellyel a Maxwell-eloszlás kísérleti igazolását adta,
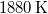-es ezüstszálról távozó atomok sebességeloszlását mérte meg, az ábrán vázolt elrendezéssel. Az 
pontbeli tengelyen elhelyezkedő szálról távozó ezüstatomok az 
nyíláson át jutottak az sugarú hengerfelületre. A berendezés 
szögsebességgel forgott, aminek következtében a 
sebességű atom az pont helyett 
-ben csapódott le.
- a) Állapítsuk meg az
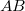ív 
hosszát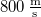 
sebességű atomok esetén, ha a fordulatszám 
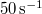és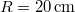 
!Végeredmény![\[x=\frac{\omega R^2}{v}\]](/images/math/0/b/6/0b64d775cd07f10acdc2f74976361052.png)
- b) Milyen sebességnél adják a legnagyobb rétegvastagságot a külső hengerfelületen lecsapódó ezüstatomok?ÚtmutatásAz időegység alatt lecsapódó részecskék számát határozzuk meg a Maxwell-eloszlás alapján, és használjuk ki az
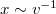összefüggést. Végeredményahol![\[v_m=\sqrt{\frac52}\,v_0,\]](/images/math/b/b/e/bbec4f31fa99ad4b348e8f27cca0b017.png)
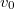a legvalószínűbb sebesség.
- a) Állapítsuk meg az
- Az
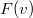sebességeloszlási függvényből a 
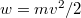összefüggés felhasználásával vezessük le az 
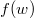energia-eloszlási függvényt, ahol 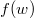azt mutatja meg, hogy az összes molekula hányadrésze rendelkezik 
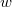és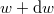 
közötti mozgási energiával! Mekkora a legvalószínűbb 
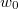energia és mennyi az átlagos kinetikus energia?Végeredmény![\[f(w)=\frac{4}{v_0\sqrt{\pi}}\frac{1}{w_v\sqrt{2\mu}}\sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\}, \text{ ahol } w_v=\frac12 \mu v_0^2=kT\]](/images/math/4/6/e/46ed18cb6e204a14b7d02f1f6f168d50.png)
![\[w_0=\frac12kT,\qquad \langle w\rangle=\frac32kT\]](/images/math/3/a/7/3a7857f15c6a811008e25cebad3e2a36.png)
- Legfeljebb mekkora lehet az
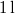térfogatú, gömb alakú edényben lévő 
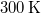-es hidrogéngáz nyomása, hogy az átlagos szabad úthossz nagyobb legyen az edény átmérőjénél? A hidrogénmolekula átmérője 
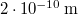.Végeredményahol![\[p<\frac{kT}{2\sqrt{2}\, R \, d^2\pi}=0{,}188\,\mathrm{Pa},\]](/images/math/f/1/3/f13f6dbd41c6c990671c0eb82ccfe194.png)
az 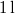-es tartály sugara.
- Hogyan változik az ideális gáz diffúziós állandója és belső súrlódási együtthatója, ha a gáz térfogata -szersére nő
- a) állandó hőmérsékleten,Végeredmény -szeres, változatlan.
- b) állandó nyomáson?Végeredmény
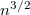-szeres, 
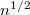-szeres.
- a) állandó hőmérsékleten,
- térfogatú, vékonyfalú tartályban ideális gáz van, az edényt légüres tér veszi körül. Feltesszük, hogy a gáz kiáramlása lassú, így a gáz egyensúlyi állapotát a folyamat nem zavarja, továbbá a lyuk mérete sokkal kisebb, mint a szabad úthossz, tehát a lyuk területére is érvényes az az összefüggés, hogy az edény falának időegység alatt nekiütköző molekulák száma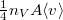
, ahol 
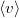a molekulák átlagsebessége. A hőmérséklet mindvégig .
- a) Hogyan változik az idő függvényében az edényben lévő gáz
részecskeszáma, ha a tartály falán igen kicsi, területű lyuk van?Végeredményahol![\[N(t)=n_0\exp\{-t/\tau\},\]](/images/math/0/f/6/0f66732b3648dd5d9e4a439bd08de0d9.png)
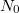a kezdeti részecskeszám-sűrűség, 
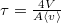. - b) Határozzuk meg azt az időtartamot, amely alatt a gáz nyomása felére csökken!Végeredmény
![\[\tau_{1/2}=\tau \ln 2\]](/images/math/8/9/8/8988e91daa948b7308b8d2c1d7b6f229.png)
- a) Hogyan változik az idő függvényében az edényben lévő gáz
- Két azonos térfogatú tartály kacsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben
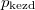nyomású, a másikban kétszer akkora nyomású hidrogéngáz van. A gázok hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos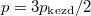 
egyensúlyi nyomás alakul ki!ÚtmutatásHasználjuk ki, hogy egyensúlyban az egyes edényekben a molekulák térfogati sűrűsége állandó, és az összes molekulák száma a folyamatban nem változik.
- Két azonos térfogatú tartály kacsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben 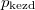nyomású hidrogéngáz, a másikban kétszer akkora nyomású oxigéngáz van. A gázok hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos 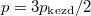egyensúlyi nyomás alakul ki!ÚtmutatásHasználjuk ki, hogy a két gáz nem hat kölcsön, alkalmazzuk a parciális nyomások tételét.
- Egy
vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó 
és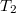 
, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért 
távolsággal, és írjuk fel a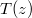 
függvényt a megadott mennyiségekkel!Végeredmény![\[T(z)=T_1+\frac{T_2-T_1}{d}z\]](/images/math/b/6/5/b6576fbfcb4cdb76f8702fbc59f78dae.png)
- Mennyi idő alatt képződik
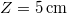vastag jégréteg egy tó felszínén, ha a léghőmérséklet 
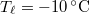, a víz hőmérséklete a jégréteg alatt 
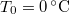? Tegyük fel, hogy a jégréteg felső felülete mindig azonos hőmérsékletű a levegővel, alső felülete pedig mindig 
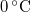-os. A jég olvadáshője 
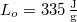, hővezetési tényezője 
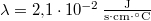, sűrűsége pedig 
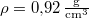.ÚtmutatásÍrjuk fel egy elemi időtartam alatt keletkező elemi vastagságú jégréteg felszabadulásakor keletkező hőt, és tegyük fel, hogy ez a jégrétegen keresztül hővezetéssel távozik, majd integráljuk a kapott egyenletet. Az analitikus megoldás érdekében hanyagoljuk el a jég fajhőjét.Végeredmény5 óra alatt képződik![\[t(Z) = \left(\frac{\rho L_o}{2\lambda(T_0-T_\ell)}\right)\,Z^2, \]](/images/math/d/8/7/d876a0a553d038419a342caf35cbffed.png)
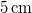vastag jégréteg.
-
hőmérsékletű, igen nagy hőkapacitású folyadékba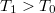 
hőmérsékletű, 
tömegű és 
fajhőjű, abszolút jó hővezető testet helyezünk a 
pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik (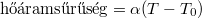
), az hőátadási tényező ismert, a test felületének nagysága . Határozzuk meg a test hőmérsékletét 
idő eltelte után!ÚtmutatásA leadott hőt fejezzük ki egyrészt a hőkapacitással, és a hőmérsékletváltozással, másrészt a folyadékba történő hőátadással, és integráljuk a kapott egyenletet.Végeredmény![\[T = T_0+\left(T_1-T_0\right)e^{\textstyle -\frac{A\alpha}{cm}t}\]](/images/math/1/3/f/13f20fc241d9d56f3b09002a2987438f.png)
