„Termodinamika példák - Ideális gáz részecskéinek energia szerinti eloszlása” változatai közötti eltérés
A Fizipedia wikiből
a |
a |
||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
<wlatex>Az [[Termodinamika példák - Stern-kísérlet|előző feladatban]] taglaltaknak megfelelően az | <wlatex>Az [[Termodinamika példák - Stern-kísérlet|előző feladatban]] taglaltaknak megfelelően az | ||
| − | $$F(v)=A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\}$$ | + | $$ F(v) = A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\} $$ |
| − | Maxwell-féle sebességeloszlás-függvény szigorúan véve egy valószínűségi sűrűségfüggvény, $v_0=\sqrt{\frac{2kT}{\mu}}$ a legvalószínűbb sebesség és $A=\frac{4}{v_0\sqrt{\pi}}$ | + | Maxwell-féle sebességeloszlás-függvény szigorúan véve egy valószínűségi sűrűségfüggvény, $v_0=\sqrt{\frac{2kT}{\mu}}$ a legvalószínűbb sebesség és $A=\frac{4}{v_0\sqrt{\pi}}$ a normáló nényező. Az energia szerinti eloszlás (matematikailag ismét csak sűrűségfüggvény) kiszámításához, egy mértéktranszformációt kell végrehajtanunk. |
Ez fizikailag azt jelenti, hogy felírjuk a gázmolekulák $[v,v+\mathrm{d}v)$ sebességintervallumba eső hányadát és ezt megfeleltetjük a $[w,w+\mathrm{d}w)$ energiaintervallumnak: | Ez fizikailag azt jelenti, hogy felírjuk a gázmolekulák $[v,v+\mathrm{d}v)$ sebességintervallumba eső hányadát és ezt megfeleltetjük a $[w,w+\mathrm{d}w)$ energiaintervallumnak: | ||
| − | $$F(v)\,\mathrm{d}v=f(w)\,\mathrm{d}w,$$ | + | $$ F(v)\,\mathrm{d}v = f(w)\,\mathrm{d}w, $$ |
ahol az intervallum kezdőpontja a | ahol az intervallum kezdőpontja a | ||
| − | $$w=\frac{1}{2}\mu {v}^{2} \qquad\Leftrightarrow\qquad v=\sqrt{\frac2\mu}\sqrt{w}$$ | + | $$ w = \frac{1}{2}\mu {v}^{2} \qquad\Leftrightarrow\qquad v=\sqrt{\frac2\mu}\sqrt{w} $$ |
| − | + | sebesség–energia-összefüggésből, hossza pedig ebből differenciálás útján kapható: | |
| − | $$ \frac{\mathrm{d}v}{\mathrm{d}w} = \sqrt{\frac2\mu} \frac1{2\sqrt{w}} \qquad\Rightarrow\qquad \mathrm{d}v=\frac{\mathrm{d}w}{\sqrt{2\mu w}}.$$ | + | $$ \frac{\mathrm{d}v}{\mathrm{d}w} = \sqrt{\frac2\mu} \frac1{2\sqrt{w}} \qquad\Rightarrow\qquad \mathrm{d}v=\frac{\mathrm{d}w}{\sqrt{2\mu w}}. $$ |
Behelyettesítés után: | Behelyettesítés után: | ||
| − | $$f\left(w\right)\mathrm{d}w = F(v)\,\mathrm{d}v= A \frac{w}{w_v} \exp\left\{ -\frac{w}{w_v} \right\} \frac{1}{\sqrt{2\mu w}}\mathrm{d}w,$$ | + | $$ f\left(w\right)\,\mathrm{d}w = F(v)\,\mathrm{d}v |
| + | = A \frac{w}{w_v} \exp\left\{ -\frac{w}{w_v} \right\} \frac{1}{\sqrt{2\mu w}}\,\mathrm{d}w,$$ | ||
azaz | azaz | ||
$$f\left(w\right) = B \sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\} ,$$ | $$f\left(w\right) = B \sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\} ,$$ | ||
| − | ahol $w_v=\frac12 \mu v_0^2=kT$ a legvalószínűbb sebességhez tartozó energia és $B=\frac{A}{w_v\sqrt{2\mu}}$. | + | ahol $w_v=\frac12 \mu v_0^2=kT$ a legvalószínűbb sebességhez tartozó energia és $B=\frac{A}{w_v\sqrt{2\mu}}$ normáló tényező. |
Mivel $f(w)$ pozitív értékkészletű, $0$-ban és $\infty$-ben lecseng, azért extrémuma egyben a $w_0$-lal jelölt legvalószínűbb energia: | Mivel $f(w)$ pozitív értékkészletű, $0$-ban és $\infty$-ben lecseng, azért extrémuma egyben a $w_0$-lal jelölt legvalószínűbb energia: | ||
| − | $$\left.\frac{\mathrm{d}f(w)}{\mathrm{d}w}\right|_{w_0}=B\exp\left\{-\frac{w_0}{kT}\right\}\left(\frac1{2\sqrt{w_0}}-\frac{\sqrt{w_0}}{kT}\right)=0.$$ | + | $$ \left.\frac{\mathrm{d}f(w)}{\mathrm{d}w}\right|_{w=w_0} = B \exp\left\{-\frac{w_0}{kT}\right\} \left(\frac1{2\sqrt{w_0}}-\frac{\sqrt{w_0}}{kT}\right) = 0. $$ |
| − | A fenti kifejezésben csak a kerek | + | A fenti kifejezésben két tényezője közül csak a kerek zárójeles lehet nulla, ennek a tényezőnek a megoldása a legvalószínűbb energia, ami éppen a legvalószínűbb sebességhez tartozó energiának a fele: |
| − | $$w_0=\ | + | $$ w_0 = \frac12 kT = \frac12 w_v. $$ |
| − | + | ||
| − | + | ||
| − | + | ||
| + | Az átlagos energiát az $f(w)$ függvény első momentuma: | ||
$$ \langle w\rangle = \int_0^\infty w f(w)\,\mathrm{d}w = B \int_0^\infty w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w.$$ | $$ \langle w\rangle = \int_0^\infty w f(w)\,\mathrm{d}w = B \int_0^\infty w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w.$$ | ||
| − | + | Ez parciális integrálással (első tényezőt deriváljuk, másodikat integráljuk) értékelhető ki: | |
$$ \langle w\rangle = \left[-B \, kT \, w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \right]_0^\infty - \frac32(-kT) \int_0^\infty B \sqrt{w}\exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w,$$ | $$ \langle w\rangle = \left[-B \, kT \, w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \right]_0^\infty - \frac32(-kT) \int_0^\infty B \sqrt{w}\exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w,$$ | ||
ahol az első tag a határokon eltűnik, az integrál pedig éppen a teljes energiaeloszlás-függvény integrálja, azaz egy normált sűrűségfüggvény integrálja, aminek értéke $1$. Ezzel a részecskék átlagos energiája | ahol az első tag a határokon eltűnik, az integrál pedig éppen a teljes energiaeloszlás-függvény integrálja, azaz egy normált sűrűségfüggvény integrálja, aminek értéke $1$. Ezzel a részecskék átlagos energiája | ||
A lap 2013. április 24., 13:40-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kinetikus gázelmélet, transzport |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az
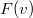sebességeloszlási függvényből a 
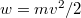összefüggés felhasználásával vezessük le az 
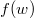energia-eloszlási függvényt, ahol 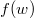azt mutatja meg, hogy az összes molekula hányadrésze rendelkezik 
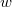és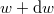 
közötti mozgási energiával! Mekkora a legvalószínűbb 
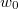energia és mennyi az átlagos kinetikus energia?
Megoldás
Az előző feladatban taglaltaknak megfelelően az
![\[ F(v) = A \left(\frac{v}{v_0}\right)^2 \exp\left\{ -\left(\frac{v}{{v}_{0}}\right)^2 \right\} \]](/images/math/c/f/5/cf5f3f3be2402240f65ad3e01eca8fdf.png)
Maxwell-féle sebességeloszlás-függvény szigorúan véve egy valószínűségi sűrűségfüggvény,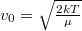 
a legvalószínűbb sebesség és 
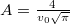a normáló nényező. Az energia szerinti eloszlás (matematikailag ismét csak sűrűségfüggvény) kiszámításához, egy mértéktranszformációt kell végrehajtanunk.
Ez fizikailag azt jelenti, hogy felírjuk a gázmolekulák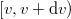 
sebességintervallumba eső hányadát és ezt megfeleltetjük a 
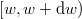energiaintervallumnak:
![\[ F(v)\,\mathrm{d}v = f(w)\,\mathrm{d}w, \]](/images/math/0/f/0/0f06e997fd28bcbee1ec9e48c4a0d805.png)
ahol az intervallum kezdőpontja a
![\[ w = \frac{1}{2}\mu {v}^{2} \qquad\Leftrightarrow\qquad v=\sqrt{\frac2\mu}\sqrt{w} \]](/images/math/1/f/1/1f10c451adc1594c6ad2e9356598b5b2.png)
sebesség–energia-összefüggésből, hossza pedig ebből differenciálás útján kapható:
![\[ \frac{\mathrm{d}v}{\mathrm{d}w} = \sqrt{\frac2\mu} \frac1{2\sqrt{w}} \qquad\Rightarrow\qquad \mathrm{d}v=\frac{\mathrm{d}w}{\sqrt{2\mu w}}. \]](/images/math/8/d/7/8d7a9b6d1e7f0fc6eb700debfe539fd2.png)
Behelyettesítés után:
![\[ f\left(w\right)\,\mathrm{d}w = F(v)\,\mathrm{d}v = A \frac{w}{w_v} \exp\left\{ -\frac{w}{w_v} \right\} \frac{1}{\sqrt{2\mu w}}\,\mathrm{d}w,\]](/images/math/8/b/4/8b4b881ebc16cce2116c18c7a55b5c06.png)
azaz
![\[f\left(w\right) = B \sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\} ,\]](/images/math/5/f/d/5fda3318193e142b95895af3c16ee03e.png)
ahol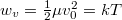 
a legvalószínűbb sebességhez tartozó energia és 
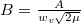normáló tényező.
Mivel 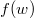pozitív értékkészletű, 
-ban és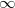 
-ben lecseng, azért extrémuma egyben a 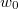-lal jelölt legvalószínűbb energia:
![\[ \left.\frac{\mathrm{d}f(w)}{\mathrm{d}w}\right|_{w=w_0} = B \exp\left\{-\frac{w_0}{kT}\right\} \left(\frac1{2\sqrt{w_0}}-\frac{\sqrt{w_0}}{kT}\right) = 0. \]](/images/math/7/5/9/7591a91b9a870d5202e6360b43d4d125.png)
A fenti kifejezésben két tényezője közül csak a kerek zárójeles lehet nulla, ennek a tényezőnek a megoldása a legvalószínűbb energia, ami éppen a legvalószínűbb sebességhez tartozó energiának a fele:
![\[ w_0 = \frac12 kT = \frac12 w_v. \]](/images/math/d/4/4/d444b8eb74b5a5b9d46de61ee339f196.png)
Az átlagos energiát az 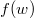függvény első momentuma:
![\[ \langle w\rangle = \int_0^\infty w f(w)\,\mathrm{d}w = B \int_0^\infty w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w.\]](/images/math/4/e/9/4e9c311b1a8efa980cc59d280899ad1d.png)
Ez parciális integrálással (első tényezőt deriváljuk, másodikat integráljuk) értékelhető ki:
![\[ \langle w\rangle = \left[-B \, kT \, w^{\frac32} \exp\left\{ -\frac{w}{kT} \right\} \right]_0^\infty - \frac32(-kT) \int_0^\infty B \sqrt{w}\exp\left\{ -\frac{w}{kT} \right\} \,\mathrm{d}w,\]](/images/math/d/9/0/d904176aeafe8e87f62da43b19a8911a.png)
ahol az első tag a határokon eltűnik, az integrál pedig éppen a teljes energiaeloszlás-függvény integrálja, azaz egy normált sűrűségfüggvény integrálja, aminek értéke 
. Ezzel a részecskék átlagos energiája
![\[\langle w\rangle=\frac32kT\]](/images/math/9/6/9/96922c0f826d15fda9c40bde74e46a45.png)
az ekvipartíció tételével összhangban.
